Note to Self

BasicGates

task1.1

サンプル

X(q);
// 0と1を反転

task1.2

サンプル

H(q);
// Hadamardで重ね合わせの状態を作る

task1.3

サンプル

Z(q);
// 符号反転

task1.4

サンプル

Ry(q);
// y軸に対する回転

参考

task1.5

サンプル

S(q);

task1.6

サンプル

R1(alpha,q);

task1.7

サンプル

Z(q);
X(q);
Z(q);
X(q);
// マイナス付与と反転を繰り返す

task1.8

サンプル

Z(qs[1]);

参考

上記参考では、最初にBellstateを作っている

task1.9

サンプル

X(qs[1]);
// どちらかのqubitに対して0と1を反転

task1.10

サンプル

X(qs[1]);
Z(qs[0]);
// task1.8とtask1.9の組み合わせ

task2.1

サンプル

CNOT(qs[0],qs[1]);
// 1qubit目を制御ビットとして2qubit目を反転

task2.2

サンプル

CZ(qs[0],qs[1]);
// 1qubit目を制御ビットとして2qubit目のプラスマイナスを反転

task2.3

サンプル

CNOT(qs[0],qs[1]);
CNOT(qs[1],qs[0]);
CNOT(qs[0],qs[1]);
// 制御ビットを入れ替えながら反転を繰り返す

補助ビットなしで入れ替えられることに感動（普通のコンピュータでは1個余分に配列を持ってないと入れ替えられない、、、と思って感動したのは認識間違いか？）

参考

task2.4

サンプル

CCNOT(qs[0],qs[1],qs[2]);
// 3qubitバージョン

task2.5

サンプル

CCNOT(qs[0],qs[1],qs[2]);
CCNOT(qs[0],qs[2],qs[1]);
CCNOT(qs[0],qs[1],qs[2]);

Superposition

task1

サンプル

H(q);

task2

サンプル

x(q);
H(q);

task3

サンプル

Ry(2.0*alpha, q);

task4

サンプル

H(qs[0]);
H(qs[1]);

task5

サンプル

H(qs[0]);
Z(qs[0]);

H(qs[1]);
S(qs[1]);

task6

サンプル

H(qs[0]);
CNOT(qs[0], qs[1]);

task7

サンプル

if (index == 0) {
  H(qs[0]);
  CNOT(qs[0], qs[1]);
}elif (index == 1) {
  X(qs[0]);
  H(qs[0]);
  CNOT(qs[0], qs[1]);
}elif (index == 2) {
  H(qs[0]);
  X(qs[1]);
  CNOT(qs[0], qs[1]);
}elif (index == 3) {
  X(qs[0]);
  H(qs[0]);
  X(qs[1]);
  CNOT(qs[0], qs[1]);
}

task8

サンプル

H(qs[0]); 
// |000000> + |100000>
// 1つ目を制御qubitにして反転を繰り返す
for(i in 1 .. Length(qs)-1){
  CNOT(qs[0], qs[i]);
}

task9

サンプル

for(i in 0 .. Length(qs) - 1){
  H(qs[i]);
}

task10

サンプル

for(i in 0 .. Length(qs) - 2){
  H(qs[i]);
}

// 最後のbitで偶奇が決まる
if(isEven != true){
  X(qs[Length(qs) - 1]);
}

task11

サンプル

let theta = ArcSin(1.0/Sqrt(3.0));
Ry(2.0 * theta, qs[0]);
// Sqrt(2/3)|00> + Sqrt(1/3)|10>

// |0> の方だけHadamard
(ControlledOnInt(0, H))([qs[0]],qs[1]);

task12

サンプル

// Controlled U
// U = e^(ia) AXBXC
// A = Rz(a)Ry(b/2)
// B = Ry(-b/2)Rz(-(c+b)/2)
// C = Rz((c-a)/2)
// AXBXC = Rz(a)Ry(b)Rz(c)
let theta1 = ArcSin(Sqrt(3.0/12.0));
let theta2 = ArcSin(Sqrt(2.0/3.0));
let theta3 = (-1.0) * ArcSin(Sqrt(1.0/2.0));

Ry(2.0*theta1, qs[0]);

CNOT(qs[0], qs[1]);
Ry((-1.0) * theta2, qs[1]);
CNOT(qs[0], qs[1]);
Ry(theta2, qs[1]);

CNOT(qs[1], qs[0]);
Ry((-1.0) * theta3, qs[0]);
CNOT(qs[1], qs[0]);
Ry(theta3, qs[0]);

Controlled Ryを使えば良かった...

task13

サンプル

H(qs[0]);
for(i in 1 .. Length(qs)-1){
  if(bits[i]){
    CX(qs[0], qs[i]);
  }
}

task14

サンプル

operation TwoBitstringSuperposition (qs : Qubit[], bits1 : Bool[], bits2 : Bool[]) : Unit {
  // ...
  // search control bit
  mutable cqb = 0;
  for(i in 0 .. Length(qs)-1){
      // |...0...> + |...1...> or |...1...> + |...0...>
      if(bits1[i] != bits2[i]){
          set cqb = i;
      }
  }
     
  // |0...0> -> |0...0...0> + |0...1...0>
  H(qs[cqb]);
  
  for(i in 0 .. Length(qs)-1){
    if(i != cqb) {
      if(bits1[i]){
        if(bits2[i]) {
        // ith qubit: |1> and [1>
          X(qs[i]);
        } else {
        // ith qubit : |1> and |0>
          if(bits1[cqb]){
          // control qubit: |...1...> + |...0...>
            CNOT(qs[cqb], qs[i]);
          } else {
          // control qubit: |...0...> + |...1...>
            X(qs[cqb]);
            CNOT(qs[cqb], qs[i]);
            X(qs[cqb]);
          }
        }
      } else {
        if(bits2[i]) {
        // ith qubit: |0> and [1>
          if(bits1[cqb]){
          // control qubit: |...1...> + |...0...>
            X(qs[cqb]);
            CNOT(qs[cqb], qs[i]);
            X(qs[cqb]);
          } else {
          // control qubit: |...0...> + |...1...>
            CNOT(qs[cqb], qs[i]);
          }
        }
      }
    }
  }
        
}

task15

サンプル

operation FourBitstringSuperposition (qs : Qubit[], bits : Bool[][]) : Unit {
  // ...
  using(auxiliary = Qubit[2]){
    // extra qubits
    for(i in 0 .. Length(auxiliary) - 1){
      H(auxiliary[i]);
    }
    // |0000>|00> + |0000>|01> + |0000>|10> + |0000>|11>
          
    for(i in 0 .. Length(qs) - 1){
    // auxiliary:|00>, |10>, |01>, |11> = |0>, |1>, |2>, |3> (ControlledOnInt)
      for(j in 0 .. 3){
        if(bits[j][i]){
          (ControlledOnInt(j, X))(auxiliary, qs[i]);
        }
      }
    }
    // |bits[0]>|00> + |bits[1]>|10> + |bits[2]>|01> + |bits[3]>|11>
          
    (ControlledOnBitString(bits[1], X))(qs, auxiliary[0]);
    // |bits[0]>|00> + |bits[1]>|00> + |bits[2]>|01> + |bits[3]>|11>
           
    (ControlledOnBitString(bits[2], X))(qs, auxiliary[1]);
    // |bits[0]>|00> + |bits[1]>|00> + |bits[2]>|00> + |bits[3]>|11>
            
    (ControlledOnBitString(bits[3], X))(qs, auxiliary[0]);
    // |bits[0]>|00> + |bits[1]>|00> + |bits[2]>|00> + |bits[3]>|01>
    (ControlledOnBitString(bits[3], X))(qs, auxiliary[1]);
    // |bits[0]>|00> + |bits[1]>|00> + |bits[2]>|00> + |bits[3]>|00>
           
  }
}

task16

サンプル

open Microsoft.Quantum.Math;
open Microsoft.Quantum.Convert;

operation WState_PowerOfTwo (qs : Qubit[]) : Unit {
  // ...
  let N = Length(qs);
  let n = Floor(Log(IntAsDouble(N))/Log(2.0));

  X(qs[0]); // |10000...>

  if(n != 0){
    for(i in 0 .. n - 1){

      let j = Floor(2.0^IntAsDouble(i));
      H(qs[j]);
      CNOT(qs[j], qs[0]);

      for(k in 1 .. j - 1){
        CCNOT(qs[0], qs[k], qs[j + k]);
        CNOT(qs[j + k], qs[0]);
        CNOT(qs[j + k], qs[k]);
        CNOT(qs[j + k], qs[j]);
      }
    }
  }
}

task17

サンプル

open Microsoft.Quantum.Math;
open Microsoft.Quantum.Convert;

operation WState_Arbitrary (qs : Qubit[]) : Unit is Adj + Ctl{
  // |W_k> = Sqrt(k-1/k) |0>|W_k-1> + Sqrt(1/k) |1>|00...0>
  let N = Length(qs);

  if(N == 1){

    X(qs[0]); // |1>

  }else{

    let theta = ArcSin(1.0 / Sqrt(IntAsDouble(N)));
    Ry(2.0 * theta, qs[0]);

    X(qs[0]);
    Controlled WState_Arbitrary ([qs[0]], qs[1 .. N - 1]);
    X(qs[0]);

  }
}

この問題を考えている途中で、Controlled HとControlled Xを使うと|10...0> + |010...0> + ...はできるが係数が違う、という残念なメモがipadに残っています...

Measurements

task1.1

サンプル

return M(q) == One;

初めての測定。

task1.2

サンプル

if(M(q) == One){
  X(q);
}

qubitを|0>の状態にせよ、とのことなので、測定して|1>なら反転。

task1.3

サンプル

// if |s> = |+>, H|s> = |0>
// if |s> = |->, H|s> = |1>
H(q);
return M(q) == Zero;

task1.4

サンプル

// |A> = Ry(2.0*alpha)|0>
// |B> = Ry(2.0*alpha)|1>
Ry((-1.0) * 2.0 * alpha, q);

return M(q) == Zero;

task1.5

サンプル

if(M(qs[0]) == One){
  return 1;
}else{
  return 0;
}

1qubit目を測定すれば区別できる。

task1.6

サンプル

if(M(qs[0]) == Zero){
  if(M(qs[1]) == Zero){
      return 0;
  }else{
      return 1;
  }
}else{
  if(M(qs[1]) == Zero){
      return 2;
  }else{
      return 3;
  }
}

1qubit目と2qubit目を測定すれば区別できる。

task1.7

サンプル

// bit値が異なる場所を探す（関数化してreturnした方が無駄がないかも）
mutable k = 0;
for(i in 0 .. Length(qs) - 1){
  if(bits1[i] != bits2[i]){
  set k = i;
  }
}

if(M(qs[k]) == Zero){
  
  if(bits1[k]){
    return 1;
  }else{
    return 0;
  }
  
}else{
  
  if(bits1[k]){
    return 0;
  }else{
    return 1;
  }
  
}

2つの状態について、何番目のqubitが異なるのかを見つければ解ける。

どこで異なるのかを見つけるのは、関数化した方が無駄な計算をしなくて良い。。。

task1.8

サンプル

let Nqubits = Length(qs);
let M1 = Length(bits1);
let M2 = Length(bits2);
mutable M12 = M1;
mutable bits = bits1;

if(M2 > M1){
  set M12 = M2;
  set bits = bits2;
}

mutable s = 0;
for(i in 0 .. Nqubits - 1){

  // すべて同じ値が入っている場所を探す
  mutable flag = 1;
  for(j in 1 .. M12 - 1){
    // フラグが1（今までは同じ値）で、j-1番目とj番目が異なる場合
    if(flag == 1 and bits[j-1][i] != bits[j][i]){
      set flag = 0;
    }
  }

  if(flag == 1){
    set s = i;
  }
}

if(M(qs[s]) == Zero){

  if(bits1[0][s]){
    return 1;
  }else{
    return 0;
  }
  
}else{
  
  if(bits1[0][s]){
    return 0;
  }else{
    return 1;
  }
  
}

task1.9

サンプル

// 測定結果を整数値に変換
let qsM = MultiM(qs);
let result = ResultArrayAsInt(qsM);

// bits1と比較
for(s in bits1){
  if(BoolArrayAsInt(s) == result){
    return 0;
  }
}

return 1;

task1.10

サンプル

let n = Length(qs);

// 1qubit目を1に変える（もしWstateなら）
for(i in 1 .. n - 1){
  CNOT(qs[i], qs[0]);
}

if(M(qs[0]) == Zero){
  return 0;
}else{
  return 1;
}

task1.11

サンプル

let n = Length(qs);

if(M(qs[0]) == One){
// 1qubit目の測定が1なら、2qubit目の測定で判定

  if(M(qs[1]) == One){
    return 0;
  }else{
    return 1;
  }

}else{
// 1qubit目の測定が0なら、2qubit目以降、1が測定されるかどうかで判定

  for(i in 1 .. n - 1){
    if(M(qs[i]) == One){
      return 1;
    }
  }

  return 0;

}

task1.12

サンプル

// |Bell0> = |00> + |11>
// |Bell1> = |00> - |11>
// |Bell2> = |01> + |10>
// |Bell3> = |01> - |10>

CNOT(qs[0], qs[1]);
// |bell0> : |00> + |10>
// |bell1> : |00> - |10>
// |Bell2> : |01> + |11>
// |Bell3> : |01> - |11>

H(qs[0]);
// |bell0> : |00>
// |bell1> : |10>
// |Bell2> : |01>
// |Bell3> : |11>
  
if(M(qs[0]) == Zero){
  if(M(qs[1]) == Zero){
    return 0;
  }else{
    return 2;
  }
}else{
  if(M(qs[1]) == Zero){
    return 1;
  }else{
    return 3;
  }
}

task1.13

// |S0> = |00> + |01> + |10> + |11>
// |S1> = |00> - |01> + |10> - |11>
// |S2> = |00> + |01> - |10> - |11>
// |S3> = |00> - |01> - |10> + |11>

H(qs[0]);
// |S0> : |00> + |01> 
// |S1> : |00> - |01>
// |S2> : |10> + |11>
// |S3> : |10> - |11>

H(qs[1]);
// |S0> : |00>
// |S1> : |01>
// |S2> : |10>
// |S3> : |11>

if(M(qs[0]) == Zero){
  if(M(qs[1]) == Zero){
    return 0;
  }else{
    return 1;
  }
}else{
  if(M(qs[1]) == Zero){
    return 2;
  }else{
    return 3;
  }
}

task1.14

サンプル

// |S0> = |00> - |01> - |10> - |11>
// |S1> = -|00> + |01> - |10> - |11>
// |S2> = -|00> - |01> + |10> - |11>
// |S3> = -|00> - |01> - |10> + |11>

H(qs[0]);
// |S0> : |10> - |01>
// |S1> : -|00> + |11>
// |S2> : -|10> - |01>
// |S3> : -|00> - |11>

CNOT(qs[0],qs[1]);
// |S0> : |11> - |01>
// |S1> : -|00> + |10>
// |S2> : -|11> - |01>
// |S3> : -|00> - |10>

H(qs[0]);
// |S0> : -|11>
// |S1> : -|10>
// |S2> : -|01>
// |S3> : -|00>

if(M(qs[0]) == Zero){
  if(M(qs[1]) == Zero){
    return 3;
  }else{
    return 2;
  }
}else{
  if(M(qs[1]) == Zero){
    return 1;
  }else{
    return 0;
  }
}

task1.15

サンプル

open Microsoft.Quantum.Math;

operation ThreeQubitMeasurement (qs : Qubit[]) : Int {

  // |S0> = (|100> + w|010> + w2|001>)/sqrt(3)
  // |S1> = (|100> + w2|010> + w|001>)/sqrt(3)

  // idea. |S0> ...Rotation... |W> ...Rotation etc... |000> ... measurement
  let theta1 = (-2.0) * PI() / 3.0;
  let theta2 = (-4.0) * PI() / 3.0;

  Rz(theta1, qs[1]);
  Rz(theta2, qs[2]);
  // |S0> : -|W>
  // |S1> : -|S0>

  let phi1 = 2.0 * ArcSin(1.0 / Sqrt(3.0));
  let phi2 = PI();
  let phi3 = PI() / 2.0;

  Controlled X([qs[2]], qs[0]);
  Controlled Ry([qs[0]], ((-1.0) * phi3, qs[2]));
  X(qs[0]);
  Controlled Ry([qs[0]], ((-1.0) * phi2, qs[1]));
  Ry((-1.0) * phi1, qs[0]);
  // if |W> then |000>

  if(M(qs[0]) == Zero){
    if(M(qs[1]) == Zero){
      if(M(qs[2]) == Zero){
        return 0;
      }
    }
  }

  return 1;

}

task2.1

サンプル

open Microsoft.Quantum.Math;

operation IsQubitPlusOrZero (q : Qubit) : Bool {

  let theta = PI() / 4.0;

  Ry(theta, q);
  // |0> : cos(theta/2)|0> + sin(theta/2)|1>
  // |+> :    (cos(theta/2) - sin(theta/2))/sqrt(2) |0> 
  //          +  (cos(theta/2) + sin(theta/2))/sqrt(2) |1>
  // |0>の方の|0>が観測される確率と|+>の方の|0>が観測される確率の差が最大になるのが、
  // theta = PI/4のとき

  if(M(q) == Zero){
    return true;
  }else{
    return false;
  }

}

task2.2

サンプル

// 単純に測定すると、1が観測されれば、|+>と判明 : 
//        確率は0.25 = 0.5(|0> or |+>) * 0.5(|+>の時に|0> or |1>)
// これだと題意に合わないので、補助ビットを加えてHadamardして補助ビットから測定すると、
// さらに上記に0.5*が入り題意に合う

mutable result = -1;

using(eq = Qubit[1]){

  H(eq[0]);

  if(M(eq[0]) == Zero){

    if(M(q) == One){
      set result = 1;
    }
  
  }else{
  
    H(q);
  
    if(M(q) == One){
      set result = 0;
    }
  
    X(eq[0]); // extra qubitを|0>に戻す
  
  }

}

return result;

task2.3

サンプル

open Microsoft.Quantum.Math;

operation IsQubitNotInABC (q : Qubit) : Int {

  mutable result = -1;

  let theta = 2.0 * ArcCos(1.0 / Sqrt(3.0));
  let phi1 = PI() / 2.0;
  let phi2 = (-1.0) * phi1;

  // Ry(-pi/2)Rx(pi/2)
  Rx(phi1, q);
  Ry(phi2, q);
  // |A> : |0>
  // |B> : 1/2 |0> - sqrt(3)/2 |1>
  // |C> : 1/2 |0> + sqrt(3)/2 |1>

  using(eq = Qubit[1]){
  // |A> : |0>|0>
  // |B> : 1/2 |0>|0> - sqrt(3)/2 |1>|0>
  // |C> : 1/2 |0>|0> + sqrt(3)/2 |1>|0>

    Controlled Rx([q], (theta, eq[0]));
    // |A> : |0>|0>
    // |B> : 1/2 |0>|0> - 1/2 |1>|0> + i/sqrt(2) |1>|1> 
    // |C> : 1/2 |0>|0> + 1/2 |1>|0> - i/sqrt(2) |1>|1>

    H(q);
    // |A> : |0>|0>
    // |B> : 1/sqrt(2) |1>|0> + i/2 |0>|1> - i/2 |1>|1> 
    // |C> : 1/sqrt(2) |0>|0> - i/2 |0>|1> + i/2 |0>|1>  

    if( M(eq[0]) == Zero ){

      if( M(q) == Zero ){
      // |0>|0> : |A> or |C>
        set result = 1;
      }else{
      // |1>|0> : |A> or |B>
        set result = 2;
      }
  
    }else{
      set result = 0;
  
      // extra qubitを|0>に戻す
      X(eq[0]);
    }

  }

  return result;

}

2週間かかった気が、、、

Controlled Rxで分子のsqrt(3)を消し、Hで|00>と|10>が消える。。。難しすぎ。。。

trine states, measurementsをキーにしてgooleもしくはgoogle scholarで検索すると色々でてくる。

katasに記載された参考文献を見てもわからなかったので、まだまだ勉強不足。

JointMeasurements

task1

サンプル

task1

サンプル

let M1 = M(qs[0]);
let M2 = M(qs[1]);

if(M1 == M2){
  return 0;
}else{
  return 1;
}

両方のqubitを測定すればわかる（操作後の状態は問わないので）

task2

サンプル

using(eq = Qubit[1]){

  CNOT(qs[0], eq[0]);
  CNOT(qs[1], eq[0]);
  // 補助qubitが
  // 0なら|00> もしくは |11>
  // 1なら|01> もしくは |10>
  
  if(M(eq[0]) == Zero){
      return 0;
  }else{
      X(eq[0]);
      return 1;
  }
  
}

ここからが本番。

操作後の状態が始状態と同じでなければならない、という点がJointMeasurementsとMeasurementsの違い。

補助qubitを使うしかないのでは・・・？

task2（Measure operationを使う）

サンプル

if(Measure([PauliZ, PauliZ], qs) == Zero){
  return 0;
}else{
  return 1;
}

Measureを使うのがJointMeasurementsでやってほしいことだと思われる。（導入部分でMeasure operationについて書いてあることに後で気が付いた。）

task3

サンプル

// 考え方はtask2と同じ
using(eq = Qubit[1]){

  CNOT(qs[0], eq[0]);
  CNOT(qs[2], eq[0]);
  // 補助qubitが
  // 0なら|0000> もしくは |1111>
  // 1なら|1100> もしくは |0011>

  if(M(eq[0]) == Zero){
    return 0;
  }else{
    X(eq[0]);
    return 1;
  }

}

Measure operationに気づく前。

task3（Measure operationを使う）

サンプル

if(Measure([PauliZ, PauliZ], [qs[1],qs[2]]) == Zero){
  return 0;
}else{
  return 1;
}

Measure operationに気づいた後。

task4

サンプル

let N = Length(qs);

using(eq = Qubit[1]){

  for(i in 0 .. N - 2){
    for(j in i + 1 .. N - 1){
      CNOT(qs[i], eq[0]);
      CNOT(qs[j], eq[0]);
    }
  }

  if(M(eq[0]) == Zero){
    return 0;
  }else{
    X(eq[0]);
    return 1;
  }
}

CNOTを繰り返せばできる（発想はtask2、task3と同じ）。

Measureを使う場合はどうすればよいのか？

task5

サンプル

if(Measure([PauliX, PauliX], qs) == Zero){
  return 0;
}else{
  return 1;
}

PauliZとPauliXなのか、PauliXとPauliXなのか・・・固有値計算を手計算。

たまには手を動かすのもいいかと・・・

task6

サンプル

H(qs[1]);
// a|00> + a|01> + b|10> + b|11>

if(Measure([PauliZ, PauliZ], qs) == One){
// この時の状態は、a|01> + b|10>
  X(qs[1]);
}

task2のMeasureを活用する。

task7

参考論文

サンプル

using(eq = Qubit[1]){

  H(eq[0]);
  
  if(Measure([PauliZ, PauliZ], [qs[0], eq[0]]) == Zero){
  // 参考論文 Table1） P1=1
      
    H(eq[0]);
    H(qs[1]);
      
    if(Measure([PauliZ, PauliZ], [qs[1], eq[0]]) == Zero){
    // 参考論文 Table1） P2=1
          
      H(eq[0]);
      H(qs[1]);
          
      // 参考論文 Table1） P1=1, P2=1, |0>A ... 何もしない
      // 参考論文 Table1） P1=1, P2=1, |1>A
      if(M(eq[0]) == One){
        X(qs[1]);
              
        // 補助qubitを|0>にする
        X(eq[0]);
      }
          
    }else{
          
      H(eq[0]);
      H(qs[1]);
          
      if(M(eq[0]) == Zero){
      // 参考論文 Table1） P1=1, P2=0, |0>A
        Z(qs[0]);
              
      }else{
      // 参考論文 Table1） P1=1, P2=0, |1>A
        Z(qs[0]);
        X(qs[1]);
              
        // 補助qubitを|0>にする
        X(eq[0]);
      }
          
    }
      
      
  }else{
  // 参考論文 Table1） P1=0
  
    H(eq[0]);
    H(qs[1]);
      
    if(Measure([PauliZ, PauliZ], [qs[1], eq[0]]) == Zero){
    // 参考論文 Table1） P2=1
          
      H(eq[0]);
      H(qs[1]);
          
      if(M(eq[0]) == Zero){
      // 参考論文 Table1） P1=0, P2=1, |0>A
        X(qs[1]);
              
      }else{
      // 参考論文 Table1） P1=0, P2=1, |1>A ... 何もしない
        // 補助qubitを|0>にする
        X(eq[0]);
      }
          
    }else{
    // 参考論文 Table1） P2=0
          
      H(eq[0]);
      H(qs[1]);
          
      if(M(eq[0]) == Zero){
      // 参考論文 Table1） P1=1, P2=1, |0>A
        Z(qs[0]);
        X(qs[1]);
              
      }else{
      // 参考論文 Table1） P1=1, P2=1, |1>A
        Z(qs[0]);
              
        // 補助qubitを|0>にする
        X(eq[0]);
      }
          
    }
  } 
}

HしたりZしたり・・・どうにもこうにもうまくいかず、Katas記載の論文を参照。

かなり冗長なコードになってるが、そこは気にしない。

Measureを2回行う、という発想はなかった。

その他

成功するまで繰り返したい

サンプル

using(eq = Qubit[1]){
  repeat{
    Reset(eq[0]);
    // プログラム
  }until(M(eq[0]) == Zero);
}

補助qbitの測定結果|0>を得るまでプログラムを実行

（参考）量子ウォークによる時系列解析, 日本評論社, 今野紀雄著

こちらの本をもとに計算してみた（私のpythonによる結果なので、あまり私の計算結果は信用しないように。確認しなければ。）

random walk

そのうち、3状態とかやってみたい（いつになるか、、、）。

1次元2状態モデル（ウォーカーが左に行くか右に行くか）
アルゴリズムは、本、もしくはこちらを参考に。
かなりざっくり言うと、評価関数を最小にするパラメータ（ウォーカーが左に動く確率）を求めて、次の時刻の位置の期待値を計算することを繰り返す。
結果1

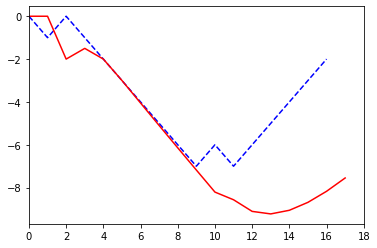
青は実際の値、赤は計算結果。
結果2

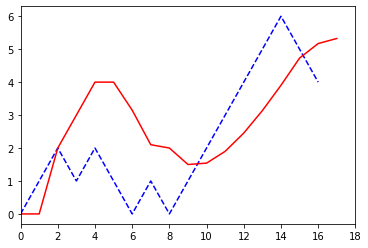
青は実際の値、赤は計算結果。
結果3

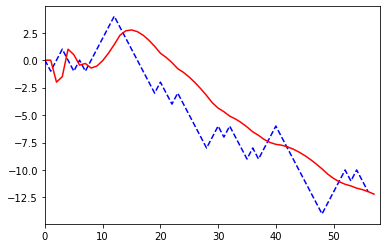
青は実際の値、赤は計算結果。
実データの場合は、値が上がったらプラス1、値が下がったらマイナス1とかにしてシミュレートする（と思っている）。

量子（特に量子コンピュータ）

BasicGates

task1.1

task1.2

task1.3

task1.4

task1.5

task1.6

task1.7

task1.8

task1.9

task1.10

task2.1

task2.2

task2.3

task2.4

task2.5

Superposition

task1

task2

task3

task4

task5

task6

task7

task8

task9

task10

task11

task12

task13

task14

task15

task16

task17

Measurements

task1.1

task1.2

task1.3

task1.4

task1.5

task1.6

task1.7

task1.8

task1.9

task1.10

task1.11

task1.12

task1.13

task1.14

task1.15

task2.1

task2.2

task2.3

JointMeasurements

task1

task1

task2

task2（Measure operationを使う）

task3

task3（Measure operationを使う）

task4

task5

task6

task7

その他

成功するまで繰り返したい

random walk