conda環境（よく使うコマンド）

いつも忘れるのでコマンドを書いておく。

パッケージインストールは、anaconda cloudで入れたいパッケージ名を調べた方が良いと思う。

環境再構築（かつ別の環境名）をするときは、利用するファイル名.ymlのnameとprefixを修正してから実行すると良い。

pythonランチャー

ファイル操作関連

conda同様いつも忘れるので書いておく。
import osが必要。

pip関連

参考

上記参考の方が詳しい。以下、簡単にメモ。

jupyter内でインストールする場合

requirements =[
    "requests"
]
for a in requirements:
    !pip install $a

venv

pythonパッケージ（ubuntuのとき）

scipy

matplotlib

pandasのgroupbyでインデックス化しない

オプション指定をしないと、groupbyで指定した変数がインデクスになるので、そうしたくない場合はas_index = Falseを追記しておく。

pandas コンソール画面出力時の小数点以下桁数を変える

pd.options.display.precision = 8

windowsでmpi4pyを使う

1. MicrosoftのサイトからMicrosoft MPIをダウンロードしてインストール
2. pathを通す（program files～Microsoft MPI～Bin）

scipy.optimize.minimize

参考

constraintsの書き方（linear）について。

\[ \begin{pmatrix} 0 \\ 0 \end{pmatrix} \le \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \le \begin{pmatrix} 1 \\ 1 \end{pmatrix} \] という場合は、以下のように行列、最小値、最大値の順番で記述する。

from scipy import optimize
linear_constraint = optimize.LinearConstraint([[1.0, 1.0], [1.0, -1.0]], [0.0, 0.0], [1.0, 1.0])
scipy.optimize.minimize(... , constraints = linear_constraint, ...)

pyodbcでMS SQLに接続

pandasデータフレームをテーブルに挿入する。

ここではサンプルデータ（id, x, dという3つの列）を用意して読み込む。nanがあると「・・・ストリームが正しくありません。・・・」みたいなエラーがでる。

import pyodbc
import pandas as pd

# read sample data
df_sample = pd.read_csv("sample_data.txt", encoding="cp932", sep="\t", dtype="object")
# replace nan to None
df_sample_fix = df_sample.where(pd.notnull(df_sample), None)

DB接続

# SQL server info
driver = "{SQL Server}"
server = 'サーバー名' 
database = 'test' 
trusted_connection = 'yes'
cnxn = pyodbc.connect('DRIVER='+driver+';SERVER='+server+';DATABASE='+database+';Trusted_Connection='+trusted_connection+';')
cursor = cnxn.cursor()

テーブルが存在するときは削除して作り直して、データフレームの値を入れる。

# create table
cursor.execute("""
               IF OBJECT_ID(N'test_table2') IS NOT NULL
               DROP TABLE test_table2

               CREATE TABLE test_table2(
               id int NOT NULL PRIMARY KEY,
               x varchar(3) NULL,
               d date NULL
               )
               """)
cnxn.commit()

# query insert
for index, row in df_sample_fix.iterrows():
    cursor.execute("""
                   INSERT INTO test_table2(id, x, d) values(?,?,?)
                   """,
                   row.id, row.x, row.d)
cnxn.commit()

cursor.close()
cnxn.close()

※別の方法として、executemanyを使うことも可能。

タプルにしてからexecutemanyを実行する。

# query insert
df_sample_fix = [tuple(x) for x in df_sample.values]
sql = """
INSERT INTO test_table2(id, x, d) values(?,?,?)
"""
cursor.executemany(sql, df_sample_fix)
cnxn.commit()

1度に実行するデータ量が多いと時間が物凄くかかる（バージョンで違う可能性あり）。適当にデータを分割してinsertしていった方が速い。

2つのリストの比較（集合演算）

setを使うと集合演算ができる。

list1 = [1,2,3,4,5]
list2 = [2,3,6]
list(set(list1) - set(list2)) #=[1, 4, 5]
list(set(list1) ^ set(list2)) #=[1, 4, 5, 6]
list(set(list1) | set(list2)) #=[1, 2, 3, 4, 5, 6]
list(set(list1) & set(list2)) #=[2, 3]

listの要素追加

listに要素を追加するときなどなど。

DataFrame行削除

dropを使って条件を満たす行を削除するときは、一旦indexを使って条件を満たす行のindexを取得し、それをリストとしてdropに渡す。

例えば、以下のようにかく（locの中に条件を入れる）。
df.drop(list(df.loc[df["x"] == 0].index))

exeファイル作成

pythonのスクリプトをexe化して実行できるようにする。pyinstallerが必要。

移動平均

1次元の場合を扱う。関数はnumpyのconvolveを使う。
validだとフィルタ部分（オプションのvの部分）の数に収まるまで計算し始めないので、結果が元の次元と異なる。
sameだとフィルタ部分がかかった部分から計算を始めるので、バイアスはかかるものの、結果は元の次元と同じになる。

できるだけ端っこにバイアスをかけたくなかったので、両端に必要数だけ同じ値（それぞれの両端の値）を追加した後、validで計算する。
（validで計算してから両端に追加しても良いと思う。）

def hokan_suruyo(list_value, num = 30):
    
    # リストをarrayに
    np_value = np.array(list_value)
    
    # validを使うために前後に値を追加（最初と最後の値を必要数だけ）
    np_value_add = np.append(np.repeat(np_value[0], num//2), np_value)
    if num % 2 == 0:
        np_value_add = np.append(np_value_add, np.repeat(np_value[-1], (num//2 - 1)))
    else:
        np_value_add = np.append(np_value_add, np.repeat(np_value[-1], num//2))

    v = np.ones(num)/num

    return list(np.convolve(np_value_add, v, mode = "valid"))

結果はこんな感じ。

# 元データ
list_test = [1, 3, 5, 7, 9, 10, 11, 13, 14, 15]

# mode = "same"の場合
list(np.convolve(np.array(list_test), [1/3, 1/3, 1/3], mode="same"))
## 結果（最後が14*1/3 + 15*1/3となって値が落ちてしまう）
### 最後：14 * 1/3 + 15 * 1/3
### 最初：1 * 1/3 + 3 * 1/3
# [1.3333333, 3.0, 5.0, 7.0, 8.666666, 10.0, 11.333333, 12.6666666, 14.0, 9.666666666]

# 関数を使った場合
hokan_suruyo(list_test, 3)
## 結果
### 最後：14 * 1/3 + 15 * 1/3 + 15 * 1/3
### 最初：1 * 1/3 + 1 * 1/3 + 3 * 1/3
# [1.666666, 3.0, 5.0, 7.0, 8.666666, 10.0, 11.3333333, 12.6666666, 14.0, 14.66666666]

convert igraph to networkx

igraphのvertexのリストとedgeのリストを抽出して、networkxのadd_nodes_fromとadd_edges_fromを使う。

# G:igraph
vertexlist = G.vs.indices
edgelist = G.get_edgelist()

# create graph
G_nx = nx.Graph()
G_nx.add_nodes_from(vertexlist)
G_nx.add_edges_from(edgelist)

pickleで保存、読取

write_pickleとRead_Pickleを使う。

import igraph as ig
# G:graph object
G.write_pickle(fname="test.plk")
G_test = ig.Graph.Read_Pickle(fname="test.plk")

最大ノード数の弱連結グループを抽出

python igraphで一番大きい弱連結グループを取り出す。

import igraph as ig
import pandas as pd

"""
edge data
"""
df_edges = pd.DataFrame({"from":[1,1,1,1,2,2,4,3,6,6,7,7,10,10], "to":[2,3,4,5,3,5,5,1,7,8,9,10,11,8]})

"""
create directed graph object
"""
G = ig.Graph.TupleList(df_edges[["from","to"]].values, directed=True)
print("G.vs, G.es:", len(G.vs), len(G.es))

# plot
ig.plot(G, "test.pdf", vertex_label = G.vs["name"])

"""
最大弱連結グループの抽出（有向グラフでなくてもよい）
"""
G_part = G.clusters(mode="weak")
num_vertices = [len(x) for x in G_part]
maxvalue = max(num_vertices)
maxindex = num_vertices.index(maxvalue)
print(G_part[maxindex])

G_sub = G.subgraph(G_part[maxindex])
ig.plot(G_sub, "test.pdf", vertex_label = G_sub.vs["name"])

最後のig.plotでpdfとして出力しているのは、spyder画面内だとラベルが表示されないため。

有効グラフと無向グラフのエッジ数の差

双方向の向きが各ノードにいくつ存在するかどうかを確認する。

import igraph as ig
import pandas as pd

df_edges = pd.DataFrame({"from":[1,1,1,1,2,2,4,3,6,6,7,7,10,10,8,10], "to":[2,3,4,5,3,5,5,1,7,8,9,10,11,8,10,7]})

G = ig.Graph.TupleList(df_edges[["from","to"]].values, directed=True) # Falseでも最終結果は同じ
G_ud_s = ig.Graph.TupleList(df_edges[["from","to"]].values, directed=False).simplify()

degree_G = G.vs.degree()
degree_G_ud_s = G_ud_s.vs.degree()
diff = [x - y for x, y in zip(degree_G, degree_G_ud_s)]
print(diff)

ネットワークコミュニティ抽出

• fastgreedy（igraphで利用可能）
• Louvain（igraphで利用可能）

• Leiden（leidenalgで利用可能、コミュニティ内の最大ノード数が指定できたりする）
  参考1 参考2

下記のクラスタリング例も参照

駅データを使ってクラスタリングしてみる

あくまでもテストなので、今のところクラスタリングしたからといって何か意味を見出そうとしてはいない。
国土数値情報ダウンロードなどと組み合わせたら・・・何かできるかな？

1. 駅データ.jpを利用（ユーザー登録必要、無料枠のデータを使う、使い易いのでありがたい）
2. 上記サイトから駅データ、接続駅データ、路線データをダウンロード
3. 接続駅データがエッジの情報となるが、station_cdをstation_g_cdに変更（新宿駅でも路線が違うと別コード扱いのため）（このため、消えている路線があるかも）
4. クラスタリング実行（Leidenを使ってみた）
5. 中心性を計算

コード例（間違っている、面倒なことをしている、などあると思う

import leidenalg
import igraph as ig
import pandas as pd

"""
read data
"""
df_edges = pd.read_csv("data\\join20200619.csv", dtype="object")[["station_cd1", "station_cd2"]]
df_vertex_name = pd.read_csv("data\\station20200619free.csv", dtype="object")[["station_cd", "station_g_cd", "station_name", "line_cd", "lon", "lat"]]
df_line_name = pd.read_csv("data\\line20200619free.csv", dtype="object")[["line_cd", "line_name"]]

# 無料版の場合、station_cdが6桁は使えない（新幹線）
df_edges = df_edges[(df_edges["station_cd1"].astype(int) >= 1000000) & (df_edges["station_cd2"].astype(int) >= 1000000)]

# station_g_cdに置き換える（df_edgesはそのままだと同じ駅でも違うコードが振られているので、同じ駅は1つのコードにしたい）
df_edges = df_edges.merge(df_vertex_name, left_on = "station_cd1", right_on = "station_cd", how = "left").drop(columns = ["station_cd", "station_name", "line_cd", "lon", "lat"])
df_edges = df_edges.rename(columns = {"station_g_cd" : "station_g_cd1"})
df_edges = df_edges.merge(df_vertex_name, left_on = "station_cd2", right_on = "station_cd", how = "left").drop(columns = ["station_cd", "station_name", "line_cd", "lon", "lat"])
df_edges = df_edges.rename(columns = {"station_g_cd" : "station_g_cd2"})
df_edges = df_edges.dropna()

# station_g_cdを使って駅名マスタを作り直す
df_vertex_name_fix = df_vertex_name.groupby("station_g_cd", as_index = False).first()

"""
create graph object
"""
G = ig.Graph.TupleList(df_edges[["station_g_cd1","station_g_cd2"]].values).simplify()
print(len(G.vs), len(G.es))

"""
crustering with leiden algorithm
"""
part = leidenalg.find_partition(G, leidenalg.ModularityVertexPartition, seed = 1, n_iterations = -1)
print(len(part), len(part.membership))
#print(part) #このときはノードの名前が表示される
#print(part[0]) #このときは0番のクラスタに含まれるノードのインデックスが表示される

"""
convert to dataframe
"""
G.vs["group"] = part.membership
G.vs["degree"] = G.vs.degree()
dict1 = dict(station_g_cd = G.vs["name"], color = G.vs["group"], degree = G.vs["degree"])
df_result = pd.DataFrame(data = dict1)

# クラスタ内ノード数の情報追加
df_result["num_node"] = df_result.groupby("color").transform("count")["station_g_cd"]

# merge station name, line name
df_result = df_result.merge(df_vertex_name_fix, on = "station_g_cd", how = "left")
df_result = df_result.merge(df_line_name, on = "line_cd", how = "left")

"""
中心性を計算
"""
degree_centrality = [x / (len(G.vs) - 1) for x in df_result["degree"].values]
eigenvector_centrality = G.evcent(scale = False)

# クラスタごとに計算してみる（クラスタ間の接続は落とす）
df_result["degree_cls"] = 0
degcent_cls_list = []
for part_tmp in part:
    G_sub = G.subgraph(part_tmp)
    tmp = G_sub.vs.degree()
    df_result["degree_cls"].iloc[part_tmp] = tmp

"""
クラスタ係数
"""
# convert to networkx
vertexname = G.vs["name"]
vertexlist = G.vs.indices
edgelist = G.get_edgelist()
## create graph
G_nx = nx.Graph()
G_nx.add_nodes_from(vertexlist)
G_nx.add_edges_from(edgelist)

# igraph
cls_coeff = G.transitivity_local_undirected(mode = "zero")
# netwrokx
cls_coeff_nx = list(nx.clustering(G_nx).values())

座標データを持っているので、QGISを使って描画してみる。

1. 以下のコードを追加して、ポイントデータとラインデータを作成する。他の方法もあるかもしれないが、エッジ情報を使うならWKT（Well-known text）が手っ取り早いと思う。

   サンプル

   """
   QGISでプロットしてみる
   """
   # ポイントデータとして
   df_result.to_csv("output\\station_data.tsv", sep = "\t", index = False)
   # ラインデータとして
   df_line = df_edges[["station_g_cd1", "station_g_cd2"]].merge(df_vertex_name_fix, left_on = "station_g_cd1", right_on = "station_g_cd", how = "left").drop(columns = ["station_g_cd", "station_cd", "station_name", "line_cd"])
   df_line = df_line.rename(columns={"lon":"lon1", "lat":"lat1"})
   df_line = df_line.merge(df_vertex_name_fix, left_on = "station_g_cd2", right_on = "station_g_cd", how = "left").drop(columns = ["station_g_cd", "station_cd", "station_name", "line_cd"])
   df_line = df_line.rename(columns={"lon":"lon2", "lat":"lat2"})
   df_line["wkt"] = "linestring(" + df_line["lon1"] + " " + df_line["lat1"] + "," + df_line["lon2"] + " " + df_line["lat2"] + ")"
   df_line["wkt"].to_csv("output\\line_wkt.tsv", sep = "\t", index = False)
   

2. 作成した2つのファイルをQGISに取り込む

   ポイントデータ

   レイヤ

   レイヤの追加

   CSVテキストレイヤの追加

   ファイルを選択、カスタム区切りでタブを選択、ポイント座標を設定して追加

   ラインデータ

   レイヤ

   レイヤの追加

   CSVテキストレイヤの追加

   ファイルを選択、WKTを選択、ジオメトリタイプをラインに設定して追加

3. ポイントデータのシンボル設定と色分け、ラインデータのシンボルと色設定

   ポイントデータ

   画面左下のレイヤで、station_dataをダブルクリックしてレイヤプロパティを開く

   シンポロジを選択してカテゴリ値による定義でクラスタリング結果を色分け

   ラインデータ

   ポイントデータと同様にレイヤプロパティを開く

   シンポロジを選択して単一定義でシンボルをtopo railwayに設定

描画例（色分けはクラスタリング結果）

こちらにqgis2webを使ってインタラクティブなマップを作成してみた結果を置いておく。起動するまで少々時間がかかる。
groupは上記コードでクラスタリング結果として使っていたcolorと同じ。

クラスタのグループごとに1つのノードとしてまとめて表示してみる。つまり、グループ内のノードのどれかが他のグループのノードとリンクしていればグループ間のリンクがあるとみなす。

"""
クラスタ間のグラフ（各グループ1つの頂点にまとめたグラフ）に直してみる
"""
# エッジデータにクラスタグループを割り当てる
df_edges_color = df_edges
df_edges_color = df_edges_color.merge(df_result[["station_g_cd", "color"]], left_on = "station_g_cd1", right_on = "station_g_cd", how = "left").drop(columns = "station_g_cd").rename(columns = {"color":"color1"})
df_edges_color = df_edges_color.merge(df_result[["station_g_cd", "color"]], left_on = "station_g_cd2", right_on = "station_g_cd", how = "left").drop(columns = "station_g_cd").rename(columns = {"color":"color2"})

# 重複したグループの組み合わせを削除する
df_edges_color = df_edges_color[["color1", "color2"]].drop_duplicates(["color1", "color2"])

# グループの中で一番degreeの大きいstation_g_cdを割り当てる
df_station_g_to_color = df_result.sort_values(["degree", "station_g_cd"],ascending=False).groupby("color", group_keys=False).head(1)

QGISで表示してみる。各クラスタの代表駅はとりあえずdegreeの大きいもの（同じ値の場合はstation_g_cdが小さいもの）にしているので、分かりづらいかもしれない。

左：全国、右：東京周辺

networkxでshapeファイルを読み込む

read_shpを使うと有向グラフとしてポイント、ラインシェープファイルを読み込むことができる。
無向グラフに変える場合は、to_undirectedを使う。

ちなみに、「import osgeo...」のエラーがでたときは、GDALをインストールする。

conda install -c conda-forge gdal

隣接ノードを取り出す

あるノードの1つ隣のノードや2つ隣のノードを取り出したい場合、igraphだとneighborhoodが使える。

# G:igraph
# 2つ隣まで
nb12_list = G.neighborhood(order = 2)
# 1つ隣まで
nb1_list = G.neighborhood(order = 1)
# 2つ隣のノードだけを各ノードについて取り出す
## 集合演算を行う
nb2_list = [list(set(x) ^ set(y)) for x, y in zip(nb12_list, nb1_list)]
## これでも同じ
nb2_list2 = G.neighborhood(order = 2, mindist = 2)

e-statの境界データを使って人口数をプロットしてみる

e-Statから境界データ（小地域）を47県分ダウンロード（zipファイル）した後、geopandasのread_fileでshapefileを読込み、pandasのconcatで結合して全国のshapefileを作成する。

zipefileを使って一時フォルダにzipを展開

import zipfile
import os

# zip展開
# DIR_DATAはダウンロードした47県分の境界データ（zipファイル）の保存場所
list_zip = os.listdir(DIR_DATA)
for file_name in list_zip:
    with zipfile.ZipFile(DIR_DATA + file_name) as myzip:
        myzip.extractall(TMP_DIR)

拡張子shpを読込み、1つのgeodataframeとして結合

import geopandas as gpd
import pyproj
from fiona.crs import from_epsg
import pandas as pd

# shpファイル読込（もっと良い書き方がありそう）
# TMP_DIRはzipfile展開先のフォルダ
epsg_num = 4612
list_files = os.listdir(TMP_DIR)
cnt = 0
for x in list_files:
    # 拡張子を分離
    base, exe = os.path.splitext(x)
    if exe == ".shp":
        if cnt == 0:
            # Read file using gpd.read_file()
            data = gpd.read_file(TMP_DIR + "\\" + x, encoding = "cp932")
            data.crs = from_epsg(epsg_num)
        else:
            tmp_data = gpd.read_file(TMP_DIR + "\\" + x, encoding = "cp932")
            tmp_data.crs = from_epsg(epsg_num)
            # データ結合
            data = pd.concat([data, tmp_data])
        
        cnt += 1

"""
shapefileを保存
"""
# Create a output path for the data
outfp = "temporary\\japan.shp"
data.to_file(outfp, encoding = "utf-8")

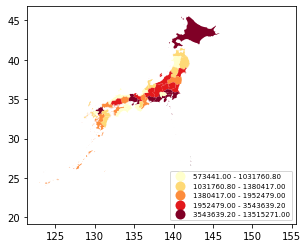
県で集約してからプロットする。

data_ken = data[["PREF", "JINKO", "geometry"]].dissolve(by = "PREF", aggfunc = "sum") # 時間がかかるよ
data_ken.plot(column = 'JINKO', scheme = 'quantiles', cmap = 'YlOrRd', legend = True, legend_kwds={"loc": "lower right", "fontsize": 7})

結果はこんな感じ。

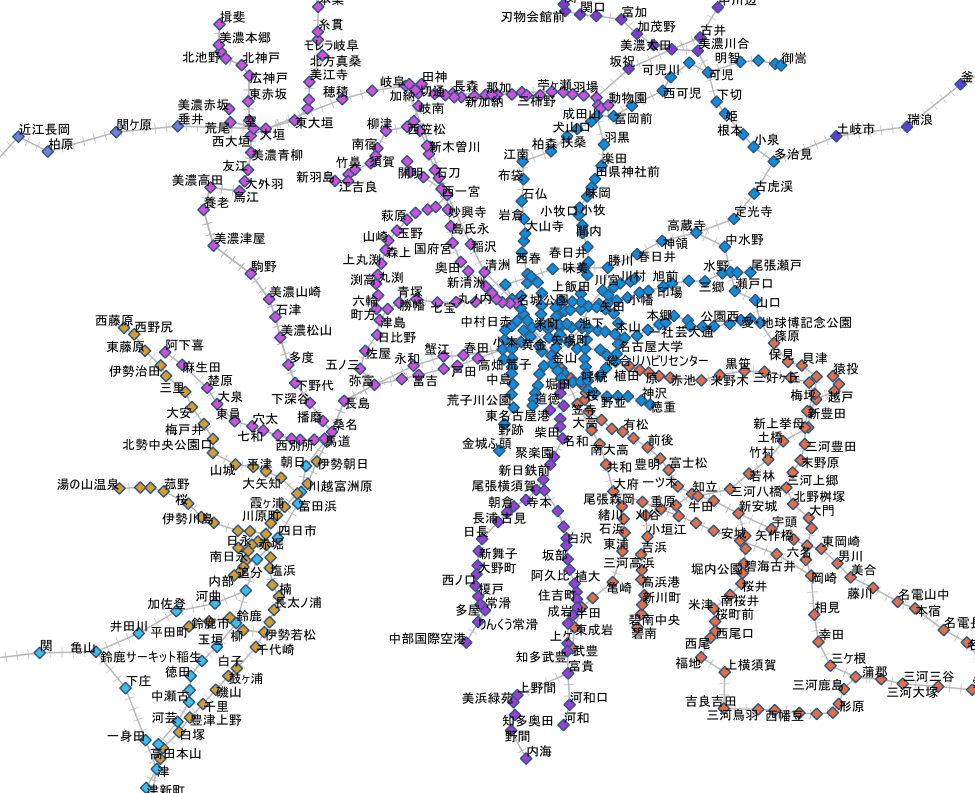
駅周辺人口などを集計して、bokehで表示

前にQGISのツールを使ってインタラクティブなwebページを作成したが、今回はbokehを使ってみた。
結果はこちら。

• 最初の関数設定はbokehでのプロット用。本当は検索窓などつけたかったが、それはまたいつか・・・
• 国勢調査2015の世帯データはe-statからダウンロード。
  pandasのread_csvはzipのまま読み込めるので、県別にダウンロードしたzipをどこかのフォルダにまとめておいておき、展開と結合をすればＯＫ。
  ちなみに、各データの2行目は日本語の列名になっているが、不要なのでスキップする。
• 駅データについてははnetworkの節を参照。GeoDataFrameに変換。
• 境界データのshapefileに世帯データをKEY_CODEでjoin。
  その前に、KEY_CODEでdissolveしておく。
  同じKEY_CODEだが、境界データが複数存在する場合があるため（ちゃんと確認していないので間違っているかも）。
• bufferを使って、半径ｘｘの円を作成。
• areaを使って、境界データの各面積を計算。
• overlayを使って、境界データを1つ上で作成した円で切り取り、その各面積を計算。
• 元の面積と切り取られた面積を利用して、人口などを計算する（各境界内に均等に人が住んでいるという仮定が入っている）。
• インタラクティブなマップの作成では、プロットの色付けを人口なのか世帯なのか、で変えたかったのでmapclassifyを使ってクラス分類をした。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import geopandas as gpd
import mapclassify
from bokeh.plotting import figure, save
from bokeh.models import ColumnDataSource, LogColorMapper
from bokeh.palettes import RdYlBu11 as palette
from bokeh.models import Circle
from bokeh.layouts import Column, Row
from bokeh.models.widgets import TableColumn, DataTable
from fiona.crs import from_epsg
from shapely.geometry import Point, Polygon, LineString, MultiLineString


"""
関数設定
"""
# インタラクティブマップの作成関数 - 選択
def bokeh_plot_select(data, data_line, palette, set_bins = "jinko"):
    
    # 並べ変え
    data = data.sort_values("bins_" + set_bins)
    data["bins"] = data["bins_" + set_bins]
    #data["value"] = data["anbun_" + set_bins]
        
    # テーブルの列選択
    select_columns = ["station_name", "line_name", "anbun_jinko", "anbun_setai",
                      "anbun_setai1", "anbun_setai2", "anbun_setai3", "anbun_setai4",
                      "anbun_setai5"]
    
    select_columns_name = ["駅名", "路線", "人口", "世帯", "世帯1人",
                           "世帯2人", "世帯3人", "世帯4人", "世帯5人"]
    
    # ラインデータ
    g_data_line = ColumnDataSource(data_line.drop("geometry", axis = 1))
    # ポイントデータ
    g_data = ColumnDataSource(data.drop("geometry", axis = 1))
    # テーブル
    tc = [TableColumn(field = c1, title = c2) for c1, c2 in zip(select_columns, select_columns_name)]
    tbl_data = DataTable(source = g_data, columns = tc, width = 700, height = 150, fit_columns=True)

    # Create the color mapper
    color_mapper = LogColorMapper(palette=palette)

    # tooltips設定
    TOOLTIPS = [
        ("station_name", "@station_name"),
        ("line_name", "@line_name"),
        #("value", "@value")
        ("jinko", "@anbun_jinko"),
        ("setai", "@anbun_setai"),
        ("setai1", "@anbun_setai1"),
        ("setai2", "@anbun_setai2"),
        ("setai3", "@anbun_setai3"),
        ("setai4", "@anbun_setai4"),
        ("setai5", "@anbun_setai5")
        ]

    # Initialize our figure
    p = figure(title="test", plot_width = 700, plot_height = 700, tooltips = TOOLTIPS, 
               tools = "pan,tap,box_zoom,box_select,reset,undo,save")
    
    # Add lines
    p.multi_line("x", "y", source = g_data_line, color="grey", line_width=0.5)

    # Add points on top (as black points)
    #p.circle('x', 'y', size=3, source=psource, color="black")
    r = p.circle("x", "y", size = 8, source = g_data, legend_field = "bins", line_color = "black", fill_color = {"field": "bins", "transform": color_mapper}, alpha = 0.6)

    r.selection_glyph = Circle(fill_color = "red", line_color = "black")
    r.nonselection_glyph = Circle(fill_alpha = 0.05, line_alpha = 0.05, fill_color = {"field": "bins", "transform": color_mapper})

    p.legend.location = "top_left"

    # 散布図
    p2 = figure(title = "scatter, x:setai1 - y:setai2", plot_width = 500, plot_height = 500,
                tools = "pan,tap,box_zoom,box_select,reset,undo,save")
    p2.line("anbun_setai1", "anbun_setai1", source = g_data, color = "yellow")
    r2 = p2.circle("anbun_setai1", "anbun_setai2", source = g_data, size = 9, fill_color = "blue")
    r2.selection_glyph = Circle(fill_color = "red")
    r2.nonselection_glyph = Circle(fill_alpha = 0.05, line_alpha = 0.05, fill_color = "blue")
    
    # Save the figure
    outfp = "tmp_map\\test_map.html"
    save(Row(Column(p, tbl_data), p2), outfp)

"""
2015国勢調査（世帯）データの読込（各県のデータは結合済み）
"""
df_setai = pd.read_csv("data\\setai2015.csv", 
                       usecols = ["KEY_CODE", "T000850001", "T000850002", "T000850003", "T000850004", "T000850005", "T000850006", "T000850007", "T000850008"],
                       dtype = {"KEY_CODE" : object, "T000850001" : np.int64, "T000850002" : np.int64,
                                "T000850003" : np.int64, "T000850004" : np.int64, "T000850005" : np.int64,
                                "T000850006" : np.int64, "T000850007" : object, "T000850008" : object})


"""
駅データの読込
"""
df_edges = pd.read_csv("data\\join20200619.csv", dtype="object")[["station_cd1", "station_cd2"]]
df_vertex_name = pd.read_csv("data\\station20200619free.csv", dtype="object")[["station_cd", "station_g_cd", "station_name", "line_cd", "pref_cd" , "lon", "lat"]]
df_line_name = pd.read_csv("data\\line20200619free.csv", dtype="object")[["line_cd", "line_name"]]

# 無料版の場合、station_cdが6桁は使えない（新幹線）
df_edges = df_edges[(df_edges["station_cd1"].astype(int) >= 1000000) & (df_edges["station_cd2"].astype(int) >= 1000000)]

# station_g_cdに置き換える（df_edgesはそのままだと同じ駅でも違うコードが振られているので、同じ駅は1つのコードにしたい）
df_edges = df_edges.merge(df_vertex_name, left_on = "station_cd1", right_on = "station_cd", how = "left").drop(columns = ["station_cd", "station_name", "line_cd", "lon", "lat"])
df_edges = df_edges.rename(columns = {"station_g_cd" : "station_g_cd1"})
df_edges = df_edges.merge(df_vertex_name, left_on = "station_cd2", right_on = "station_cd", how = "left").drop(columns = ["station_cd", "station_name", "line_cd", "lon", "lat"])
df_edges = df_edges.rename(columns = {"station_g_cd" : "station_g_cd2"})
df_edges = df_edges.dropna()

# station_g_cdを使って駅名マスタを作り直す
df_vertex_name_fix = df_vertex_name.groupby("station_g_cd", as_index = False).first()
df_vertex_name_fix = df_vertex_name_fix.merge(df_line_name, on = "line_cd", how = "left")

# 路線データ
df_line = df_edges[["station_g_cd1", "station_g_cd2"]].merge(df_vertex_name_fix, left_on = "station_g_cd1", right_on = "station_g_cd", how = "left").drop(columns = ["station_g_cd", "station_cd", "station_name", "line_cd"])
df_line = df_line.rename(columns={"lon":"lon1", "lat":"lat1"})
df_line = df_line.merge(df_vertex_name_fix, left_on = "station_g_cd2", right_on = "station_g_cd", how = "left").drop(columns = ["station_g_cd", "station_cd", "station_name", "line_cd"])
df_line = df_line.rename(columns={"lon":"lon2", "lat":"lat2"})
## 型変換
df_line["lon1"] = df_line["lon1"].astype(str).astype(float)
df_line["lat1"] = df_line["lat1"].astype(str).astype(float)
df_line["lon2"] = df_line["lon2"].astype(str).astype(float)
df_line["lat2"] = df_line["lat2"].astype(str).astype(float)


"""
駅データ（ポイントデータ）をgeopandasでgeodataframeに変換
"""
# 全国
df = df_vertex_name_fix.copy()
gdf = gpd.GeoDataFrame(df, geometry = gpd.points_from_xy(df["lon"].astype(str).astype(float), df["lat"].astype(str).astype(float)))
# crsの設定
gdf.crs = from_epsg(4612)
print(gdf.crs)


"""
駅データ（ラインデータ）をgeopandasでgeodataframeに変換
"""
shp_line = [LineString([(df_line.loc[i, "lon1"], df_line.loc[i, "lat1"]), (df_line.loc[i, "lon2"], df_line.loc[i, "lat2"])]) for i in range(len(df_line))]
gdf_line = gpd.GeoDataFrame(df_line, geometry = shp_line)
gdf_line.crs = from_epsg(4612)
print(gdf_line.crs)

"""
shapefileを読込
"""
# 全国
fp = "temporary\\japan.shp"
gdf_base_org = gpd.read_file(fp, encoding = "utf-8")

# KeyCodeでdissolve
gdf_base_org = gdf_base_org[["KEY_CODE", "PREF", "CITY", "JINKO", "SETAI", "X_CODE", "Y_CODE", "geometry"]].dissolve(by = "KEY_CODE", aggfunc = "sum") # 時間がかかるよ

# 世帯データ結合(元々intだったのにfloatとなるが問題ない)
gdf_base_org = gdf_base_org.merge(df_setai, on = "KEY_CODE", how = "left")

# key_codeの頭5桁を使って集約（小地域だと細かいため）
#gdf_base_org["key_code_city"] = gdf_base_org["KEY_CODE"].str[:5]
#gdf_base = gdf_base_org[["key_code_city", "JINKO", "geometry"]].dissolve(by = "key_code_city", aggfunc = "sum") # 時間かかるよ
# 集約しない
gdf_base = gdf_base_org.copy()


"""
駅データとベースをプロットしてみる
注意！全国の場合にプロットすると大変！せめて、市区町村などで集約してからにすること！
"""
#ax = gdf_base.plot(facecolor='gray')
#gdf.plot(ax=ax, color='red', markersize = 0.1)


"""
座標系変換
"""
gdf_org = gdf.copy()
gdf = gdf.to_crs(epsg = 6933)
gdf_base = gdf_base.to_crs(epsg = 6933)


"""
駅から半径1kmの円を作成
"""
gdf["geometry"] = gdf["geometry"].buffer(distance = 1000)


"""
重なっている部分を抽出
"""
# 元の市区町村での面積を計算しておく
gdf_base["area_base"] = gdf_base.area

# 重なっている部分の面積を計算
intersection = gpd.overlay(gdf, gdf_base, how='intersection')
intersection["area_intersection"] = intersection.area

# 面積按分で人口を計算（関数化した方がいいか）
intersection["anbun_jinko"] = intersection["JINKO"] * intersection["area_intersection"] / intersection["area_base"]

# 面積按分で世帯を計算
intersection["anbun_setai"] = intersection["T000850001"] * intersection["area_intersection"] / intersection["area_base"]
intersection["anbun_setai1"] = intersection["T000850002"] * intersection["area_intersection"] / intersection["area_base"]
intersection["anbun_setai2"] = intersection["T000850003"] * intersection["area_intersection"] / intersection["area_base"]
intersection["anbun_setai3"] = intersection["T000850004"] * intersection["area_intersection"] / intersection["area_base"]
intersection["anbun_setai4"] = intersection["T000850005"] * intersection["area_intersection"] / intersection["area_base"]
intersection["anbun_setai5"] = intersection["T000850006"] * intersection["area_intersection"] / intersection["area_base"]

# station_g_cd毎に集約
res_anbun = intersection.groupby(["station_g_cd"], as_index = False).sum(["anbun_jinko", "anbun_setai", "anbun_setai1", "anbun_setai2", "anbun_setai3", "anbun_setai4", "anbun_setai5"])

# 元の駅ポイントデータにジョイン
gdf_res = gdf.merge(res_anbun[["station_g_cd", "anbun_jinko", "anbun_setai", "anbun_setai1", "anbun_setai2", "anbun_setai3", "anbun_setai4", "anbun_setai5"]], on = "station_g_cd", how = "left")
gdf_org_res = gdf_org.merge(res_anbun[["station_g_cd", "anbun_jinko", "anbun_setai", "anbun_setai1", "anbun_setai2", "anbun_setai3", "anbun_setai4", "anbun_setai5"]], on = "station_g_cd", how = "left")


"""
プロットしてみる
"""
# 座標系をもとに戻す
gdf_res = gdf_res.to_crs(epsg = 4612)
gdf_base = gdf_base.to_crs(epsg = 4612)

#ax = gdf_base.plot(facecolor='gray')
#gdf_res.plot(ax = ax, column="anbun_jinko", scheme="Fisher_Jenks", k=9, cmap="RdYlBu", linewidth=0, legend=True, legend_kwds={"loc": "upper left", "fontsize": 8})

gdf_res.plot(column="anbun_jinko", scheme="quantiles", cmap="RdYlBu", linewidth=0, legend=True, legend_kwds={"loc": "upper left", "fontsize": 8})


"""
インタラクティブなマップを作成してみる
"""
# 色分けのためのクラス分類
class_res = mapclassify.Quantiles(gdf_res["anbun_jinko"], k = 11)
gdf_res["group_jinko"] = class_res.yb
gdf_res["bins_jinko"] = class_res.bins[gdf_res["group_jinko"]]

# 色分けのためのクラス分類（世帯） -- 関数化したほうがいい
class_res = mapclassify.Quantiles(gdf_res["anbun_setai"], k = 11)
gdf_res["group_setai"] = class_res.yb
gdf_res["bins_setai"] = class_res.bins[gdf_res["group_setai"]]

class_res = mapclassify.Quantiles(gdf_res["anbun_setai1"], k = 11)
gdf_res["group_setai1"] = class_res.yb
gdf_res["bins_setai1"] = class_res.bins[gdf_res["group_setai1"]]

class_res = mapclassify.Quantiles(gdf_res["anbun_setai2"], k = 11)
gdf_res["group_setai2"] = class_res.yb
gdf_res["bins_setai2"] = class_res.bins[gdf_res["group_setai2"]]

class_res = mapclassify.Quantiles(gdf_res["anbun_setai3"], k = 11)
gdf_res["group_setai3"] = class_res.yb
gdf_res["bins_setai3"] = class_res.bins[gdf_res["group_setai3"]]

class_res = mapclassify.Quantiles(gdf_res["anbun_setai4"], k = 11)
gdf_res["group_setai4"] = class_res.yb
gdf_res["bins_setai4"] = class_res.bins[gdf_res["group_setai4"]]

class_res = mapclassify.Quantiles(gdf_res["anbun_setai5"], k = 11)
gdf_res["group_setai5"] = class_res.yb
gdf_res["bins_setai5"] = class_res.bins[gdf_res["group_setai5"]]

# x, y列作成 - ポイント
gdf_res["x"] = gdf_res["lon"].astype(str).astype(float)
gdf_res["y"] = gdf_res["lat"].astype(str).astype(float)

# x, y列作成 - ライン
gdf_line["x"] = [[gdf_line.loc[i, "lon1"], gdf_line.loc[i, "lon2"]] for i in range(len(gdf_line))]
gdf_line["y"] = [[gdf_line.loc[i, "lat1"], gdf_line.loc[i, "lat2"]] for i in range(len(gdf_line))]

# インタラクティブマップ作成
bokeh_plot_select(gdf_res, gdf_line, palette, "jinko") # jinko, setai, setai1, ...

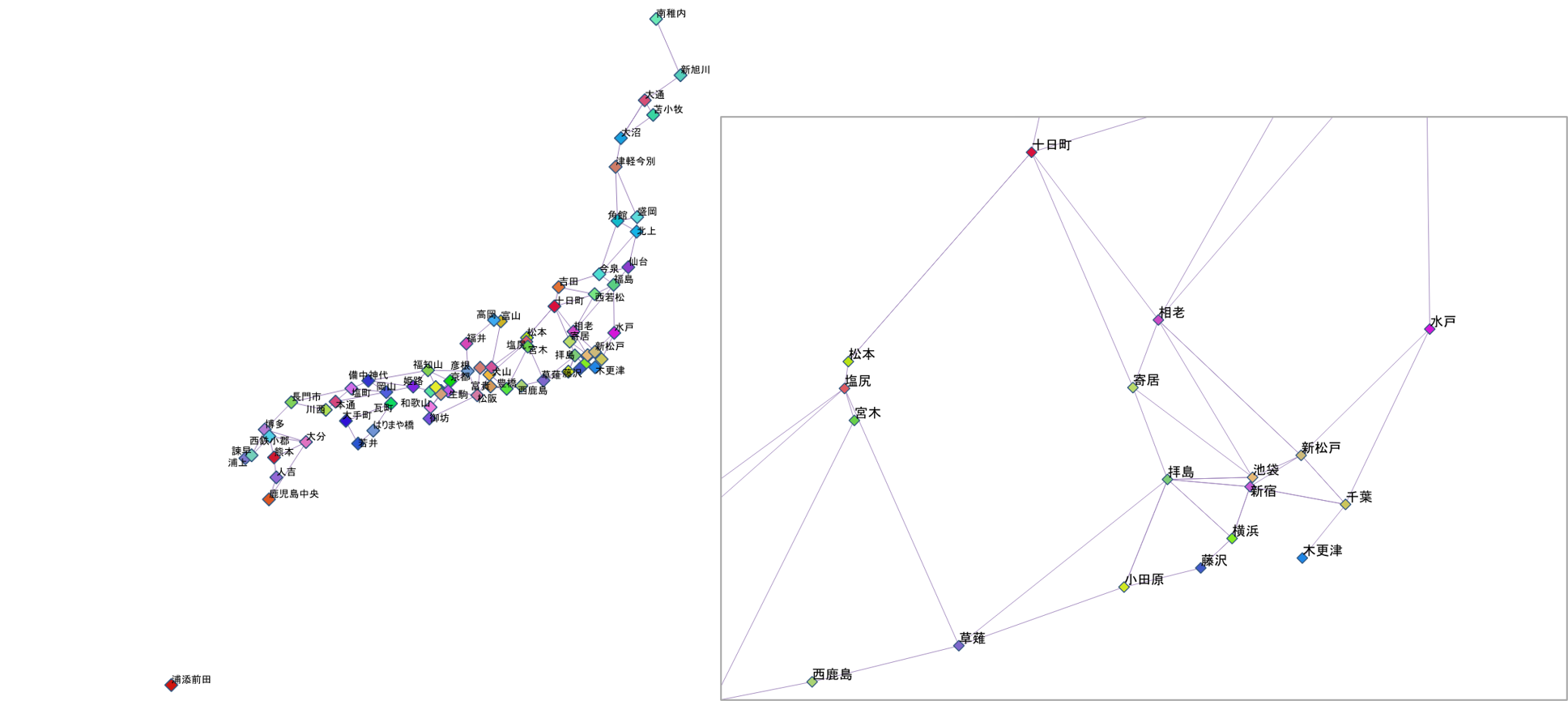
結果はこちらからみることができる。
色は、人口をmapclassify.Quantilesで11個に分類。凡例の数値は分類範囲の最大値となっている。
円（駅のこと）にカーソルを合わせると詳細がポップアップで表示される。
円をクリックした場合は、赤色になり、他のテーブルやグラフもクリックした駅がハイライトされる。

一応、いくつかの駅について、jSTAT MAPを使って、半径1kmの円の人口や世帯数を按分集計した結果と比較してみた。
値は大きくずれていないよう（値が1000ずれるとかはなさそう）なのでとりあえず良しとしよう・・・。

標高を取得

国土地理院から取得することができる。
負荷をかけ過ぎないように注意。

# lon, latともにリスト形式で入っているとして
import requests
url = "http://cyberjapandata2.gsi.go.jp/general/dem/scripts/getelevation.php?lon=" + str(list_lon[0]) +"&lat=" + str(list_lat[0]) + "&outtype=JSON"
rq = requests.get(url, timeout = 5)
rq.json()

Google APIでポイントを道路に射影

Google Roads API のNearest Roadsを使ってjson形式の結果を取得する際のメモ。

import urllib
import json

"""
google apiの基本url設定
APIキーの設定
"""
api_key = "Google Platformで取得したAPIキー"
base_url = "https://roads.googleapis.com/v1/nearestRoads?"

"""
座標パラメータ作成
以下の例は昭和記念公園付近の座標（ただし、道路上にない）
"""
list_lon = [139.40845853122605, 139.40401679328315]
list_lat = [35.70222763895725, 35.70111243532612]

# googleのドキュメントに沿って、lat, lonの順にカンマで結合し、さらにその緯度経度の組を縦棒で結合する
list_cod = [str(y)+","+str(x) for x, y in zip(list_lon, list_lat)]
api_points = "|".join(list_cod)

"""
google api実行
"""
# apiパラメータの設定
api_param = {"points": api_points, "key": api_key}

# リクエスト実行
api_paramStr = urllib.parse.urlencode(api_param)
readObj = urllib.request.urlopen(base_url + api_paramStr)
res = readObj.read()
res = json.loads(res.decode("utf8"))

# 結果
res["snappedPoints"][0]["location"]
res["snappedPoints"][1]["location"]

geopandasでポイントを道路に射影

こちらを参考。

ちなみに、道路データはOpenStreetMapなどから取得可能。（OpenStreetMapはこちら）

# gdf_line_clip:ポイントデータ付近のLineStringデータ(overlay等を使って取得しておく）
# gdf_point：ポイントデータ
gdf_line_clip_union = gdf_line_clip.geometry.unary_union
gdf_point_prg = gdf_point.copy()
# 射影
gdf_point_prg["geometry"] = gdf_point_prg.apply(lambda row: gdf_line_clip_union.interpolate(gdf_line_clip_union.project(row.geometry)), axis=1)
# shpファイルとして保存
gdf_point_prg.to_file(r"result.shp")

GPUを使うまで

参考（※2020年3月）

• Anacondaインストール
• Anaconda Prompt：pip install tensorflow（新しいバージョンはcpuとgpuが一緒になったらしい）
• cuda対応GPUカードを確認（PCを買う場合は先にこれを見ておかないといけないことに気づく）
  ※ちなみにGTX 1650が見当たらなかったが動作してよかった。
• NVIDIA GPUドライバインストール：NVIDIA GEFORCE EXPERIENCEを起動して、[ドライバー]タブの更新プロブラムの確認の隣にあるボタンをクリック、「Studioドライバ」に変更
• CUDA ツールキットのインストール（Version 10.1）※必要なら、先にVisual Studioをインストールしておく
• cuDNN SDKをダウンロード、zipを解凍してProgram FIles→NVIDIA GPU Computing Toolkit→CUDA→vx.xのフォルダ内にコピー（既に存在しているものは消さない）
• FashionMNISTを試してみる：model.fitを実行するときにGPUを使うハズ
  ※GPUの動作を見るのはこちら

• GPUが認識されているかどうかは、以下のコマンドでも見れる

  サンプル

  print("Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))
  

model.predictでエラー

複数チャンネルの画像1枚を予測しようとしたら、こんなエラー

原因は、元の画像のshapeが(a, b, c)だとしたら、(1, a, b, c)というように1個次元を増やす必要があった。

解決：np.expand_dims(a, 0)とする

Allocator・・・エラー

バッチサイズの見直しが必要だった。

This is probably because・・・エラー

（これが原因か定かではないが）GPUメモリをすべて確保されないように、tf.config.experimental.set_memory_growthを使ったらエラーがでなくなった。

マルチタスク学習

よくわかってないが）パラメータの共有方法は2つあるらしい（参考）。

• Hard parameter sharing（イメージしやすい、同じパラメータを持つ層を使う）
• Soft parameter sharing（イメージしにくい、異なるパラメータだが似ているようなパラメータを持つ層ができる、似ているような・・・距離的に近いとか）

Segmentation

PyTorchの学習済みモデルを利用して、物体検出ができる。試してみたがすごい。

• 参考1
• 参考2

ポリシー反復法

（参考）ITエンジニアのための強化学習理論入門, 中井悦司著, 技術評論社

参考の第3章。
基本的なコード（1次元、2次元グリッドワールド）は同じ。 プロットについてだけseabornではなくmatplotlibを利用した。

# ポリシーマップ作成
# 参考本ではseabornで、関数名がdraw_heatmap, draw_policy
# ここでは矢印と色を同時に表示
def draw_policy_2D(world, subplot = None, title = "Values"):
    
    if not subplot:
        fig = plt.figure(figsize = (world.size * 0.8, world.size * 0.8))
        subplot = fig.add_subplot(1, 1, 1)
    
    data_matrix = np.array([[world.value[(i, j)] for i in range(world.size)] for j in range(world.size)])
    for (x, y) in world.traps:
        data_matrix[y][x] = None

    # ヒートマップ
    im = subplot.imshow(data_matrix, cmap = "jet")
    fig.colorbar(im)
    subplot.set_title(title)
    # グラフ内に値を書き込む
    ys, xs = np.meshgrid(range(data_matrix.shape[0]), range(data_matrix.shape[1]), indexing='ij')
    for (x, y) in zip(xs.flatten(), ys.flatten()):
        if (x, y) in world.traps:
            ar = None
        elif (x, y) == world.goal:
            ar = None
        elif world.policy[((x, y), (-1, 0))] == 1:
            ar = "←"
        elif world.policy[((x, y), (0, -1))] == 1:
            ar = "↑"
        elif world.policy[((x, y), (1, 0))] == 1:
            ar = "→"
        elif world.policy[((x, y), (0, 1))] == 1:
            ar = "↓"
        
        plt.text(x, y, ar, horizontalalignment='center', verticalalignment='center')

10x10のグリッドワールドで、トラップが6列目の上から5つ、アルファが0.4の場合で描画すると下のような感じになる。
（左上がスタートで、右下がゴール。トラップに落ちると、0.4の確率でスタートに戻り、0.6の確率でゴールに移動する。）

逆行列

• 余因子
• 余因子展開
• 余因子行列
• 逆行列

単回帰分析

Rのlmとpredictで出力できるが、切片0の時の予測区間はどうなるのかふと気になったので確かめてみた。

• nヶの観測値 \begin{align}(x_i, y_i) \; i = 1, 2,\cdots , n\end{align}
• 切片ゼロの推定式 \begin{align} y_i= \beta x_i + \epsilon_i \; (i=1,\cdots, n) \\ E(\epsilon_i)=0, V(\epsilon_i)=\sigma^2, 互いに無相関 \end{align}
• 偏差平方和 \begin{align} \sum_i (y_i - \beta x_i)^2 \end{align}
• 偏差平方和を最小にする \(\hat{\beta}\) (最小2乗推定量) \begin{align} \hat{\beta} = \frac{\sum_i x_i y_i}{\sum_i x_i^2} \end{align}
• \(\hat{\beta}\)の期待値と分散 \begin{align} E(\hat{\beta}) &= \frac{\sum_i x_i E[y_i]}{\sum_i x_i^2} = \frac{\sum_i x_i \beta x_i}{\sum_i x_i^2} = \beta \\ V(\hat{\beta}) &= V\left(\frac{\sum_i x_i y_i}{\sum_i x_i^2}\right) = \frac{V(x_1 y_1) + \cdots + V(x_n y_n)}{(\sum_i x_i^2)^2} = \frac{\sum_i x_i^2 V(y_i)}{(\sum_i x_i^2)^2} = \frac{\sigma^2}{\sum_i x_i^2} \end{align}
• \((x_0, y_0)\)の新しいデータに対する、予測値\(\hat{y_0} = \hat{\beta}x_0\)の予測誤差\(y_0 - \hat{y_0}\)の期待値と分散 \begin{align} E(y_0 - \hat{y_0}) &= 0 \\ V(y_0 - \hat{y_0}) &= V(y_0) + V(\hat{y_0}) = \sigma^2 + V(\hat{\beta})x_0^2 = \sigma^2 \left(1 + \frac{x_0^2}{\sum_i x_i^2}\right) \\ \longrightarrow y_0 - \hat{y_0} &\sim N \left( 0, \sigma^2 \left(1 + \frac{x_0^2}{\sum_i x_i^2}\right) \right) \end{align}
• 信頼係数\((1 - \alpha^{\ast})\times 100\% \)の\(y_0\)の予測区間(s:残差) \begin{align} \hat{y_0} \pm t \left(\frac{\alpha^{\ast}}{2}, n - 1 \right) s \sqrt{1 + \frac{x_0^2}{\sum_i x_i^2}} \end{align} 通常は自由度n-2だが、パラメータが1つ減ったのでn-1となる。 ルートの中の切片のパラメータ由来の\(1/n\)が無くなる。

エクセルで計算したものとRの結果を比較してみる。

• エクセルの設定
  （C列は、直線の値から適当にずらすため、I列16は自由度：データ数-1） \begin{align} B列 &= 5.64 \times A列 \\ C列 &= B列 + 0.5 \times RANDBETWEEN(0,A列)*(-1)^{RANDBETWEEN(0,1)} \\ D列 &= A列 \times B列 \\ E列 &= A列 \times A列 \\ F列 &= A列 / sum(E列) \\ G列 &= A列 \times sum(D列)/sum(E列) \\ H列 &= (G列 - C列)^2 \\ I列 &= T.INV.2T(0.05,16) \\ J列 &= G列 - I列 * SQRT(sum(H列)/16) * SQRT(1+E列/sum(E列)) \\ K列 &= G列 + I列 * SQRT(sum(H列)/16) * SQRT(1+E列/sum(E列)) \end{align}
  数値例 \begin{align} \begin{array}{c|cccc} 行番号 & A列 & ... & J列 & K列 \\ 1 & x & ... & 95\%下側 & 95\%上側 \\ \hline 2 & 15 & ... & -146.935 & 319.249 \\ 3 & 40 & ... & -3.427 & 462.929 \\ 4 & 107 & ... & 380.790 & 848.376 \\ 5 & 55 & ... & 82.640 & 549.174 \\ 6 & 38 & ... & -14.905 & 451.431 \\ 7 & 88 & ... & 271.890 & 739.014 \\ 8 & 260 & ... & 1256.110 & 1730.650 \\ 9 & 351 & ... & 1775.400 & 2256.725 \\ 10 & 150 & ... & 627.084 & 1096.047 \\ 11 & 234 & ... & 1107.563 & 1580.521 \\ 12 & 575 & ... & 3049.748 & 3555.586 \\ 13 & 547 & ... & 2890.741 & 3392.943 \\ 14 & 394 & ... & 2020.449 & 2505.641 \\ 15 & 758 & ... & 4087.164 & 4620.390 \\ 16 & 442 & ... & 2293.750 & 2783.742 \\ 17 & 66 & ... & 145.738 & 612.439 \\ 18 & 99 & ... & 334.943 & 802.323 \end{array} \end{align}

• Rコード例
  （エクセルのA列とC列をコピーしてタブ区切りのテキストファイルを保存）

  サンプル

  d = read.table("sample.tsv", sep="\t", header=TRUE)
  d_lm = lm(y ~ x - 1, data=d)
  summary(d_lm)
  d_predict = predict(d_lm, interval = "prediction", level=0.95)
  

  
  結果
  \begin{align} \begin{array}{ccc} fit & lwr & upr \\ \hline 86.157 & -146.935 & 319.249 \\ 229.751 & -3.427 & 462.929 \\ 614.583 & 380.790 & 848.376 \\ 315.907 & 82.640 & 549.174 \\ 218.263 & -14.905 & 451.432 \\ 505.452 & 271.890 & 739.014 \\ 1493.380 & 1256.110 & 1730.650 \\ 2016.063 & 1775.400 & 2256.726 \\ 861.565 & 627.084 & 1096.047 \\ 1344.042 & 1107.563 & 1580.521 \\ 3302.667 & 3049.748 & 3555.586 \\ 3141.842 & 2890.741 & 3392.943 \\ 2263.045 & 2020.449 & 2505.641 \\ 4353.777 & 4087.164 & 4620.390 \\ 2538.746 & 2293.750 & 2783.742 \\ 379.089 & 145.738 & 612.439 \\ 568.633 & 334.943 & 802.324 \\ \end{array} \end{align}

  fit（予測値）、lwr（予測区間下側）、upr（予測区間上側）をG列、J列、K列と比較すると一致してるハズ。

ロジット・プロビット

（参考）現代数理統計学の基礎, 久保川 達也, 共立出版, 2017

目的変数yが2値の場合を考える。
ex）雨が降る（y = 1)、雨が降らない（y = 0)

• n個のデータ（i = 1,2, ..., n）とk個の説明変数 \[ (y_1, \boldsymbol{x}_1), ... , (y_n, \boldsymbol{x}_n) \] \[ y_i = \begin{cases} 1 \\ 0 \end{cases} \] \[ \boldsymbol{x}_i = (1, x_{1i}, ... , x_{ki})^T \]
• 回帰係数ベクトル：\( \boldsymbol{\beta} = (\beta _0, ... , \beta _n)^T \)

線形回帰の時は、\( y_i = \boldsymbol{x}_i^T \boldsymbol{\beta} + (誤差項) \) （誤差項は、重回帰だと正規分布）という形で考えていたが、今はyが0か1を取るので\( y_i \)と\( \boldsymbol{x}_i^T \boldsymbol{\beta} \) を別の形で関連付ける。

そこで、線形回帰の形はそのままで、以下のように少し考え方を変える。

• モデル：\( y_i^{\ast } = \boldsymbol{x}_i^T \boldsymbol{\beta} + u_i \)
• \( -u_i \) の分布関数：\( F(\bullet ) \)
• \( y_i = \begin{cases} 1 & y_i^{\ast} \ge 0 \\ 0 & y_i^{\ast} \lt 0 \end{cases} \)

こうすると、 \[ P(y_i = 1) = p_i = P(y_i^{\ast } \ge 0) = P(-u_i \le \boldsymbol{x}_i^T \boldsymbol{\beta} ) = F(\boldsymbol{x}_i^T \boldsymbol{\beta}) \] となってyが1になる確率が0から1の間を取り、\( \boldsymbol{x}_i^T \boldsymbol{\beta} \) が無限大に近づくにつれyが1になる確率は1に近づく。

\( F(x) \) （上記の場合\( x \)に\( \boldsymbol{x}_i^T \boldsymbol{\beta} \) が入る）の例として挙げられるのがプロビットモデルやロジットモデルとなる。

• プロビットモデル \[ F(x) = \Phi (x) = \int_{-\infty}^x \frac{1}{\sqrt{2\pi}} exp(\frac{-z^2}{2}) dz \]
• ロジットモデル \[ F(x) = \frac{exp(x)}{1 + exp(x)} \]

ロジットモデルのいいところは、対数オッズ \( log(\frac{p_i}{1-pi}) \) が\( \boldsymbol{x}_i^T \boldsymbol{\beta} \) という簡単な形になるところ。

回帰係数ベクトルの決め方は、尤度関数から最尤推定量を求める。
尤度関数は、\( y_i \) が互いに独立でベルヌーイ分布に従っていることから、 \[ L(\boldsymbol{\beta} \mid \boldsymbol{y}) = \prod_{n}^{i} p_i^{y_i} (1 - p_i)^{(1-y_i)} \] \[ logL = \sum_{i}^{n} \{ y_i logp_i + (1 - y_i)log(1 - p_i) \} \] となり、対数尤度関数について\( \boldsymbol{\beta} \) の偏微分が0になる値を計算すればよい。

試しに、1変数のときのロジスティックモデルを計算してみる。

• \( p_i = \frac{exp(\beta_1 x_{1i} + \beta_0)}{1 + exp(\beta_1 x_{1i} + \beta_0) } \)
  \( log p_i = \beta_1 x_{1i} + \beta_0 - log(1 + exp(\beta_1 x_{1i} + \beta_0)) \)
• \( 1 - p_i = \frac{1}{1 + exp(\beta_1 x_{1i} + \beta_0) } \)
  \( log (1 - p_i ) = -log(1 + exp(\beta_1 x_{1i} + \beta_0)) \)
• \( \frac{\partial log p_i }{\partial \beta_1} = x_{1i} (1 - p_i) \)
  \( \frac{\partial log p_i }{\partial \beta_0} = 1 - p_i \)
• \( \frac{\partial log (1 - p_i )}{\partial \beta_1} = - x_{1i} p_i \)
  \( \frac{\partial log (1 - p_i )}{\partial \beta_0} = - p_i \)
• \( \frac{\partial logL}{\partial \beta_1 } = \sum_{i}^{n} (y_i x_{1i} - x_{1i} p_i ) = 0 \)
  \( \frac{\partial logL}{\partial \beta_0 } = \sum_{i}^{n} (y_i - p_i ) = 0 \)

最後の2つの式をニュートン法などを使って求める。以下、pythonのコード例。ヤコビ行列まで求めても良いが、method = "krylov"は近似解（数値微分）を使って自動計算してくれる。

scipy.optimize.rootはこちらを参考

• サンプルデータは気象庁の過去の気象データ・ダウンロードを使った。
  東京＞日平均気温、降水量の日合計、日平均蒸気圧、日平均雲量＞直近1ヶ月（2020年10月5日から2020年11月5日まで）
• python statsmodelsのlogitの結果（summaryを抜粋）
  
• python scipy.optimizeの結果（回帰係数ベクトル\( \beta_0, \beta_1 \) ）
  [-4.8500086 0.31359248]

coefとscipy.optimizeの結果を見ると一致している。

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.formula.api import logit
import math
from scipy import optimize

"""
データの初期加工
"""
df_org = pd.read_csv("data\\tenki_tokyo.csv", skiprows = 3, encoding = "cp932")

# 1行目は不要
df_org = df_org.iloc[1:,:]

# 降水量の合計と平均蒸気圧を取り出す
df = df_org.iloc[1:,[4, 8]]

# 列名変更
df.columns = ["mm", "hPa"]

# nanが含まれる行は削除
df = df.dropna()

# 降水量が0より大きい時はフラグ1, 他はフラグ0
df["mm_flag"] = df["mm"].apply(lambda x : 1 if x > 0 else 0)

# プロットしてみる
plt.scatter(df["hPa"], df["mm_flag"])

"""
ロジットモデル
"""
# 回帰式
formula = "mm_flag ~ hPa"

# モデル
res_logit = logit(formula, data = df).fit()

# 結果表示
print(res_logit.summary())
dir(res_logit)

plt.scatter(df["hPa"], res_logit.predict())


"""
optimize.rootによって回帰係数を算出
"""
# ロジスティック分布の分布関数
def F(x):
    return math.exp(x) /(1 + math.exp(x))

# 解を求める関数
def fun(b, x, y):
    xb = [xi * b[1] + b[0] for xi in x]
    return [sum([yi * xi - xi * F(xbi) for xi, yi, xbi in zip(x, y, xb)]),
            sum([yi - F(xbi) for yi, xbi in zip(y, xb)])]

# beta0, beta1の初期値
initial_guess = [0, 0]
# 観測値
arg = (df["hPa"].tolist(), df["mm_flag"].tolist())
# 解を求める
sol = optimize.root(fun, [0, 0], method = "krylov", args = arg)

# 結果表示
print(sol.x)

ロジットモデル（続き）

statsmodelsとscikit learnで使うときのメモ。

statsmodelsの方は、formulaを使う方法とそうでない方法（目的変数と説明変数をデータで指定する方法）を試した。
scikit learnの注意点として、statsmodelsと同じ結果を得るにはC（inverse of regularization strength）の値を設定しないと、過学習を抑えるための正則化が効くため結果が異なる。 逆数なので、値を大きくすると正則化をしない、ということになる。

以下、サンプルコード。データは前の気象データを利用した。

import pandas as pd
from statsmodels.formula.api import logit
from sklearn.linear_model import LogisticRegression
import statsmodels.api as sm
import statsmodels.formula.api as smf

"""
ダウンロードした気象データを利用（割愛）
"""

"""
ロジットモデル
statismodels
"""
# 回帰式
formula = "mm_flag ~ hPa"

# モデル
res_logit = logit(formula, data = df).fit()
res_logit2 = smf.glm(formula, data = df, family = sm.families.Binomial()).fit()
Y = df["mm_flag"].values
X = df["hPa"].values
X = sm.add_constant(X)
res_logit3 = sm.GLM(Y, X, family = sm.families.Binomial()).fit()

# 結果表示
print(res_logit.summary())
print(res_logit2.summary())
print(res_logit3.summary())

"""
ロジットモデル
sklearn.linear_model
"""
lr = LogisticRegression(solver = "newton-cg", C=1e8)
lr.fit(df["hPa"].values.reshape(-1,1), df["mm_flag"])
print(lr.intercept_, lr.coef_)

scikit learnでreshape(-1,1)をしているのは、説明変数が1つの場合に、何も処理せずデータフレームの1列を指定すると以下のエラーが出てくるため。

ロジットモデル（続き2）

上記で試した1変数の計算について、サンプルに偏りがある場合を試す。

サンプルに偏りがあるときは、カテゴリごとに重みをつけて最尤推定量を求める。
i番目のデータの重みを \( w_i \) としたとき、次のように対数尤度の和の中に \( w_i \) をかける。 \[ logL = \sum_{i}^{n} w_i \{ y_i logp_i + (1 - y_i)log(1 - p_i) \} \]

重みは、scikit learnに倣ってclass_weight = balancedで考えてみる。 \[ 重みw_{k} = \frac{n}{2 n_{k}}, (k = 0, 1) \] \( n \) はデータ数、\( n_{k} \) は、カテゴリが0もしくは1の時のデータ数、分母の2はカテゴリの数を表す。
\( y_i = 0 \) であれば、重みは\( w_0 \) の値を使い、\( y_i = 1 \) であれば、重みは\( w_1 \) の値を使う。
（ここの添え字の意味は、カテゴリを表しているので注意。）

対数尤度を偏微分して、最終的に解くべき式は \[ \frac{\partial logL}{\partial \beta_1 } = \sum_{i}^{n} w_i (y_i x_{1i} - x_{1i} p_i ) = 0 \] \[ \frac{\partial logL}{\partial \beta_0 } = \sum_{i}^{n} w_i (y_i - p_i ) = 0 \] となるので、これをscipy.optimizeを使って計算してみる。statsmodelsの結果と一致しているハズ。

"""
ロジット statsmodels
重みあり
"""
# 重みの計算
n = len(df)
n0 = len(df[df["mm_flag"]==0])
n1 = len(df[df["mm_flag"]==1])
wi = [n/(2.0 * n0), n/(2.0 * n1)]

# 回帰式
formula = "mm_flag ~ hPa"

df["weight"] = [ wi[x] for x in df["mm_flag"].values ]

# モデルフィット
res_logit_w = smf.glm(formula, data = df, family = sm.families.Binomial(), var_weights = df["weight"].values).fit()
print(res_logit_w.summary())

"""
ロジット sklearn
重みあり
"""
lr = LogisticRegression(solver = "newton-cg", C = 1e8, class_weight = "balanced")
lr.fit(df["hPa"].values.reshape(-1, 1), df["mm_flag"])
print(lr.intercept_, lr.coef_)

lr_pred = lr.predict(df["hPa"].values.reshape(-1, 1))

"""
optimize.root
重みあり
"""
# 解を求める関数
def fun(b, x, y, w):
    xb = [xi * b[1] + b[0] for xi in x]
    return [sum([wi * yi * xi - wi * xi * F(xbi) for xi, yi, xbi, wi in zip(x, y, xb, w)]),
            sum([wi * yi - wi * F(xbi) for yi, xbi, wi in zip(y, xb, w)])]

# beta0, beta1の初期値
initial_guess = [0, 0]
# 観測値
arg = (df["hPa"].tolist(), df["mm_flag"].tolist(), df["weight"].tolist())
# 解を求める
sol = optimize.root(fun, [0, 0], method = "krylov", args = arg)

# 結果表示
print(sol.x)

プロビットモデル

statsmodelsでプロビットモデルを実行するとき。
上記ロジスティック回帰でのモデルフィット実行時のプログラムを下記にする（リンク関数の設定）。

sm.GLM(Y, X, family = sm.families.Binomial(statsmodels.genmod.families.links.probit())).fit()

主成分分析

多次元のデータを圧縮してデータを要約する。

例えば、2次元のデータを1次元に圧縮する場合、回帰直線を引くことに似ているが、回帰直線と違う点は、回帰直線で言うところの誤差がデータの各点と直線の距離で表され、各点の距離の総和が最小となる直線上にデータを集約する。
各点の距離の総和が最小となる直線を引く、というのは座標軸を1本引き直すというイメージでもいいと思う。新しい軸では説明しきれなかった残りの部分は、その軸に対して垂直に引いた軸で表す。
（分散が最大となる軸とそれに垂直な軸でもある。）（イメージは、回帰直線よりもSVMの方が近いか？）

多次元のデータの場合は、上記作業を繰り返すことで、データを最大限要約した軸、その次に要約した軸、・・・という形で、変数の数だけ軸を引くことができる。
結局座標変換しただけではないかとなるのだが、ある程度の軸でデータはほぼほぼ説明できている（例えば80パーセント説明できている）とすれば、次元を減らすことができたことになる。
使い方としては、例えば、目的変数1個に対して説明変数が10個あった時に、まずは説明変数を主成分分析によって2個の変数に要約し、その2変数でもって回帰をする、など。

具体的に計算してみる

問題の定式化

2次元に戻って、、、n個のデータ \( \boldsymbol{x}_1 = (x_{11}, x_{21}), ... , \boldsymbol{x}_n = (x_{1n}, x_{2n}) \) で計算してみる。ここでn個のデータは各変数（添え字の左側1, 2）毎に標準化されている（平均0、分散1）とする。
尚、標準化ではなく、各変数について各変数の平均値を引いた値を利用する場合もある。

新しい軸方向の単位ベクトルを \( \boldsymbol{a} = (a_1, a_2)^T , a_1^2 + a_2^2 = 1 \) とすると、\( \boldsymbol{a} \) 方向の長さは内積 \( \boldsymbol{x}_i \cdot \boldsymbol{a} \) となるので、n個の点と直線の距離の総和Lは、 \[ L = \sum_{i = 1}^{n} \{ \boldsymbol{x}_i^2 - (\boldsymbol{x}_i \cdot \boldsymbol{a})^2 \} = \sum_{i = 1}^{n} \{x_{1i}^2 + x_{2i}^2 - (a_1 x_{1i} + a_2 x_{2i})^2 \} \] で表される。よって、Lについて \( a_1^2 + a_2^2 = 1 \) の条件の下で最小化する問題になり、ラグランジュ未定乗数法を使って解いてみる。

ラグランジュ乗数を\( \lambda \)としてLを書き直し、未知数（ここでは \( a_1, a_2 \) ）で偏微分した結果を0とすると、 \[ L = \sum_{i = 1}^{n} \{x_{1i}^2 + x_{2i}^2 - (a_1 x_{1i} + a_2 x_{2i})^2 \} + \lambda (a_1^2 + a_2^2 - 1) \] \[ \frac{\partial L}{\partial a_1} = \sum_{i = 1}^{n} \{-2x_{1i} (a_1 x_{1i} + a_2 x_{2i}) \} + 2 a_1 \lambda = 0 \] \[ \frac{\partial L}{\partial a_2} = \sum_{i = 1}^{n} \{-2x_{2i} (a_1 x_{1i} + a_2 x_{2i}) \} + 2 a_2 \lambda = 0 \] となり、下2つの式は次のように書ける（✩)。 \[ a_1 \sum_{i = 1}^{n} x_{1i}^2 + a_2 \sum_{i = 1}^{n} x_{1i} x_{2i} = a_1 \lambda \] \[ a_1 \sum_{i = 1}^{n} x_{1i} x_{2i} + a_2 \sum_{i = 1}^{n} x_{2i}^2 = a_2 \lambda \] \( x_{1i}, x_{2i} (i = 1, ... , n) \) はそれぞれ標準化されていて、\( \frac{1}{n} \sum_{i = 1}^{n} x_{1i}^2 = 1 \)、\( \frac{1}{n} \sum_{i = 1}^{n} x_{2i}^2 = 1 \)、\( \frac{1}{n} \sum_{i = 1}^{n} x_{1i} x_{2i} = \rho \) （\( \rho \) は相関係数）なので、 \[ \begin{pmatrix} 1 & \rho \\ \rho & 1 \end{pmatrix} \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} = \lambda ^{\prime} \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \] \[ \lambda ^{\prime} = \frac{\lambda}{n} \] 相関行列の固有値、固有ベクトルを求める問題となる。
（各変数について平均値を引いた値を使うと、分散共分散行列になる。）

固有値、固有ベクトルを算出

固有方程式を解くと、 \[ \begin{vmatrix} 1 - \lambda^{\prime} & \rho \\ \rho & 1 -\lambda^{\prime} \end{vmatrix} = 0 \Leftrightarrow (\lambda^{\prime} - (1 - \rho))(\lambda^{\prime} - (1 + \rho)) = 0 \] \(\lambda^{\prime} = 1 + \rho \)、\(\lambda^{\prime} = 1 - \rho \) が求まる。

• \(\lambda^{\prime} = 1 + \rho = \lambda_1 \) のとき：\(a_2 = a_1 \)
• \(\lambda^{\prime} = 1 - \rho = \lambda_2 \) のとき：\(a_2 = -a_1 \)

各\(\lambda \) の値によってLの値を調べてみると \[ L = 2n - n(a_1^2 + a_2^2) - 2a_1 a_2 n \rho = n - 2a_1 a_2 n \rho \]

• \(\rho \gt 0 \)
  • \(\lambda_1 \gt \lambda_2 \)
  • \(\lambda_1 \)のとき：\(a_1 a_2 \rho \gt 0 \)
  • \(\lambda_2 \)のとき：\(a_1 a_2 \rho \lt 0 \)
  • \(L_{\lambda_1} \lt L_{\lambda_2} \)
  • \(\lambda_1 \) の方がLをより最小化している。
• \(\rho \lt 0 \)
  • \(\lambda_1 \lt \lambda_2 \)
  • \(\lambda_1 \)のとき：\(a_1 a_2 \rho \lt 0 \)
  • \(\lambda_2 \)のとき：\(a_1 a_2 \rho \gt 0 \)
  • \(L_{\lambda_1} \gt L_{\lambda_2} \)
  • \(\lambda_2 \) の方がLをより最小化している。

固有値の大きさの順に第1主成分、第2主成分とする。
相関係数が正のときは45度線、負のときは135度線上に要約していることがわかる（第1主成分）。

その他確認1：固有値の大きさについて

固有値の大きさが\(\boldsymbol{a} \) 軸上でのデータの分散を表していることをみてみる。

各データを\(\boldsymbol{a} \) 方向に射影すると\(\boldsymbol{x_i} \cdot \boldsymbol{a} \) なので、 \[ 平均 = \sum_{i=1}^{n} (\boldsymbol{x_i} \cdot \boldsymbol{a}) = a_1 \sum_{i=1}^{n} x_{1i} + a_2 \sum_{i=1}^{n} x_{2i} = 0 \] \[ 分散 = \frac{1}{n} \sum_{i=1}^{n} (\boldsymbol{x_i} \cdot \boldsymbol{a})^2 = \frac{1}{n} \sum_{i=1}^{n} (a_1 x_{1i} + a_2 x_{2i})^2 \] 既に導出した（✩）の2式について、上側は両辺に\(a_1 \)、下側は両辺に\(a_2 \)をかけて足すと、 \[ \sum_{i = 1}^{n} (a_1 x_{1i} + a_2 x_{2i})^2 = (a_1^2 + a_2^2) \lambda = \lambda \] 従って、分散は \[ 分散 = \frac{\lambda}{n} = \lambda^{\prime} \] となって固有値が新しい軸方向の分散を表していることがわかる。

その他確認2：固有ベクトルについて

求めた固有ベクトル同士が直行することを確認する。

各固有値に対応する固有ベクトルを\(\boldsymbol{a}_{\lambda_1} \)、\(\boldsymbol{a}_{\lambda_2} \)、相関行列を\(\Lambda \)とする。相関行列は対称行列であることを利用して、 \[ \lambda_2 (\boldsymbol{a}_{\lambda_1} \cdot \boldsymbol{a}_{\lambda_2}) = \boldsymbol{a}_{\lambda_1}^T (\lambda_2 \boldsymbol{a}_{\lambda_2}) = \boldsymbol{a}_{\lambda_1}^T \Lambda \boldsymbol{a}_{\lambda_2} = \boldsymbol{a}_{\lambda_1}^T \Lambda^T \boldsymbol{a}_{\lambda_2} = (\Lambda \boldsymbol{a}_{\lambda_1})^T \boldsymbol{a}_{\lambda_2} = \lambda_1 \boldsymbol{a}_{\lambda_1}^T \boldsymbol{a}_{\lambda_2} \] \[ \therefore (\lambda_2 - \lambda_1)(\boldsymbol{a}_{\lambda_1} \cdot \boldsymbol{a}_{\lambda_2}) = 0 \] よって、\(\lambda_2 \neq \lambda_1 \) なので \(\boldsymbol{a}_{\lambda_1} \cdot \boldsymbol{a}_{\lambda_2} = 0 \) が確認できた。

以上で2次元の場合の計算を終える。
n次元の場合も同様に考えることができ、求めた固有値を大きい順に\(\lambda_1, ... ,\lambda_n \) とするとm番目までの累積寄与率 \(\sum_{i=1}^{m}\lambda_i \diagup \sum_{i=1}^{n}\lambda_i \) が例えば80%を超えるところまで使えば、n次元をm次元に圧縮することができる。

pythonで確認

numpyのlinalgとstatsmodelsで結果を確認。標準化はこちらを参考。

import numpy as np
from numpy import linalg as LA
import matplotlib.pyplot as plt
from statsmodels.multivariate.pca import PCA

def zscore(x, axis = None):
    xmean = x.mean(axis=axis, keepdims=True)
    xstd  = np.std(x, axis=axis, keepdims=True)
    zscore = (x-xmean)/xstd
    return zscore

"""
データ
エクセルで、適当に作成 A1 * 0.5 + 5 + 150*rand()
"""
d = np.array([[10,98.5154296175729],[15,63.1450483672864],[22,104.601779632835],
             [36,83.4331175286678],[50,69.8319075005125],[79,126.627515802706],
             [80,113.645201788066],[90,77.2643594891816],[111,101.983352852064],
             [153,222.813109084359],[163,187.663782478305],[170,163.480044147356],
             [195,127.441561043671],[201,230.179879087941],[220,210.809659431224],
             [240,201.899825444139],[275,183.29439824263],[282,251.941927155307],
             [295,255.470330805841],[301,191.008115658807],[333,295.240661571767],
             [350,256.962051026721],[351,313.314488702949],[373,299.825847701057],
             [390,323.11892805577]]
             )

# plot
plt.scatter(d[:,0], d[:,1])


"""
標準化
"""
d_norm = zscore(d, axis=0)

"""
PCA
"""
# 相関行列
A = np.dot(d_norm.T, d_norm) * (1.0/len(d_norm))

# 固有値、固有ベクトル計算
eigval, eigvec = LA.eig(A)
print(eigval)
print(eigvec)

# statsmodelsで確認
pc = PCA(d_norm, standardize = False, demean = False, normalize = False)
#pc = PCA(d, standardize = True)
print(pc.eigenvals / len(d_norm))
print(pc.eigenvecs)

分位点回帰

（参考）高次元データ分析の方法, 安藤 知寛, 朝倉書店, 2014

分位点の分析に興味がある場合に活用。
例えば、金融資産ポートフォリオリスク管理において、ポートフォリオ収益率の下側5パーセント等のモデリングをすることで、どのような経済リスクファクターにポートフォリオ収益率が敏感なのか分析する、など。

p次元説明変数 \( \boldsymbol{x} \) が与えられたもとで、目的変数 \( y \) の条件付分布関数、条件付\( \tau \) 分位点を次のように考える。 \[ P(Y \le y \mid \boldsymbol{x}) = F(y \mid \boldsymbol{x}) \] \[ Q_{\tau}(y \mid \boldsymbol{x}) = inf \{y \mid F(y \mid \boldsymbol{x}) \ge \tau \} \] このとき、分位点回帰モデルは、 \[ Q_{\tau}(y \mid \boldsymbol{x}) = \boldsymbol{\beta}(\tau )^T \boldsymbol{x} \] \[ \boldsymbol{\beta}(\tau ) = (\beta_0 (\tau), \beta_1 (\tau), ... , \beta_p (\tau))^T \] \[ \boldsymbol{x} = (1, x_1, x_2, .... , x_p)^T \] とかける。 n個の観測データ \( (\boldsymbol{x}_i, y_i) (i=1,2,...,n) \) が与えられたとすると、\( \beta(\tau) \) は下記損失関数を最小にするような値で推定する。 \[ L = \sum_{i=1}^n \rho_{\tau}(y_i - \boldsymbol{\beta}(\tau)^T \boldsymbol{x}_i) = \sum_{y_i - \boldsymbol{\beta}(\tau)^T \boldsymbol{x}_i \lt 0}(\tau - 1) (y_i - \boldsymbol{\beta}(\tau)^T \boldsymbol{x}_i) + \sum_{y_i - \boldsymbol{\beta}(\tau)^T \boldsymbol{x}_i \ge 0}\tau (y_i - \boldsymbol{\beta}(\tau)^T \boldsymbol{x}_i) \] \[ \rho_{\tau}(u) = ( \tau - \delta(u \lt 0))u \] \( \delta(a) \) は\( a \) が成立するとき1, 成立しないとき0の値を取る（デルタ関数）。

Lの最小値をscipy.optimizeを使って求めた結果と、statsmodelsの結果を比較してみた。
Lの最小値の求め方は、線形計画問題（あるいはその双対問題）として解く方法もあるようだ。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import optimize
import statsmodels.api as sm
import statsmodels.formula.api as smf
import random

"""
データ
エクセルで、適当に作成 A1 * 0.5 + 5 + 150*rand()
"""
d = pd.DataFrame(data = 
                 np.array([[10,98.5154296175729],[15,63.1450483672864],[22,104.601779632835],
                           [36,83.4331175286678],[50,69.8319075005125],[79,126.627515802706],
                           [80,113.645201788066],[90,77.2643594891816],[111,101.983352852064],
                           [153,222.813109084359],[163,187.663782478305],[170,163.480044147356],
                           [195,127.441561043671],[201,230.179879087941],[220,210.809659431224],
                           [240,201.899825444139],[275,183.29439824263],[282,251.941927155307],
                           [295,255.470330805841],[301,191.008115658807],[333,295.240661571767],
                           [350,256.962051026721],[351,313.314488702949],[373,299.825847701057],
                           [390,323.11892805577]]
                          ),
                 columns = ["x", "y"]
                 )

# plot
plt.scatter(d["x"], d["y"])


"""
最適化する関数
"""
def fun(b, x, y, tau):
    ua = [yi - (xi * b[1] + b[0]) for xi, yi in zip(x, y)]
    la = [(tau - 1) * uai if uai < 0 else tau * uai for uai in ua]
    return sum(la)

# 分位点設定
tau = 0.3
# beta0, beta1の初期値
initial_guess = [1.0, 1.0]
# 観測値
arg = (d["x"].tolist(), d["y"].tolist(), tau)
# 解を求める
sol = optimize.minimize(fun, initial_guess, args = arg, method = "Nelder-Mead")

print(sol)

"""
statsmodels
"""
mod = smf.quantreg("y ~ x", d)
res = mod.fit(q = tau)
print(res.summary())

sum(res.resid)


"""
plot
"""
get_y = lambda a, b: a + b * d["x"]

plt.scatter(d["x"], d["y"])
y_res = get_y(res.params["Intercept"], res.params["x"])
plt.plot(d["x"], y_res, color = "red")

statsmodelsだとt-valueやp値まで出ているがこの求め方については調べてみないと。まだわかっていない。